

今回の記事では線形代数で非常に重要になってくる内容を各項目ごとにまとめていきます。
詳細な解説については関連記事を貼っていくので、そちらも参考にしてみてくださいね。
ではいきましょう!
目次
重要ポイント1. 行列・行列の計算について
行列とは簡単に言えば数字が羅列された箱のようなもの。
例えば次のようなものが行列です。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
-1 & 2 \\
4 & -5 \\
\end{array}
\right]$$
この行列は横が2行、縦が2列なので2行2列の行列または2×2行列と言います。
また、こちらの行列は横が3行、縦が4列なので3行4列の行列または3×4行列と言います。
$$\boldsymbol{B} = \left[
\begin{array}{rrr}
-1 & 20 & 3 & 2 \\
4 & -5 & 600 &21 \\
7 & 8 & -9 & 5 \\
\end{array}
\right]$$
また、行列は型が同じであれば数字と同じように足し算引き算をすることが出来ます。
例えば次の2つの行列はどちらも3×3行列で型が同じなので足し算と引き算が出来るわけですね。
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 2 & 3 \\
4 & -5 & 8 \\
7 & 2 & -9
\end{array}
\right],\boldsymbol{B} = \left[
\begin{array}{rrr}
1 & 4 & 2 \\
7 & -5 & 6 \\
2 & 3 & -4
\end{array}
\right]$$
$$\boldsymbol{A+B} = \left[
\begin{array}{rrr}
0 & 6 & 5 \\
11 & -10 & 14 \\
9 & 5 & -13
\end{array}
\right],\boldsymbol{A-B} = \left[
\begin{array}{rrr}
-2 & -2 & 1 \\
-3 & 0 & 2 \\
5 & -1 & -5
\end{array}
\right]$$

行列の足し算引き算や特殊な行列についてはこちらの記事に詳しくまとめています。

例えば行列\(A\)と行列\(B\)において、\(A\)の列の個数と\(B\)の行の個数が等しい場合かけ算をすることができます。
例えば次の2つの行列をかけ算してみましょう。
$$\boldsymbol{A}= \left[
\begin{array}{rrr}
-1 & 2 & 3 \\
4 & -5 & 6\\
\end{array}
\right],\boldsymbol{B} =\left[
\begin{array}{rrr}
-1 & 2 \\
4 & 3 \\
1 & 5 \\
\end{array}
\right]$$
まずは\(A\)の1行目、\(B\)の1列目について計算していきます。
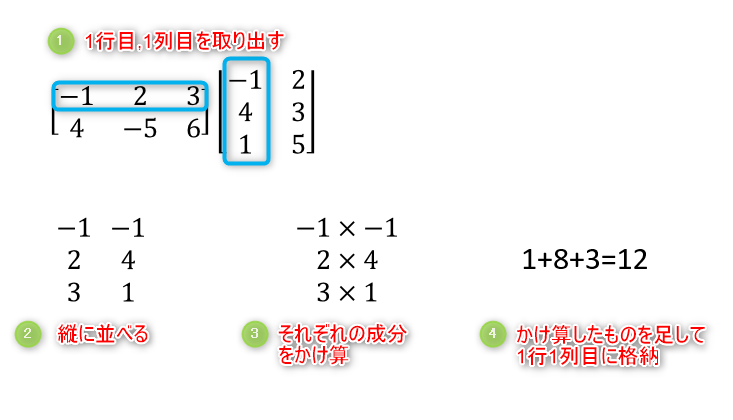
これで\(A\)の1行目、\(B\)の1列目の計算は完了です!
続いて\(A\)の1行目、\(B\)の2列目について計算していきましょう。

この計算を2行1列目、2行2列目も同様に行っていくと最終的に\(AB\)は以下のようになります。
$$\boldsymbol{AB} = \left[
\begin{array}{rr}
12 & 19 \\
-18 & 23 \\
\end{array}
\right]$$
これで行列のかけ算をすることが出来ました!
行列のかけ算は慣れが必要な部分でもあるのでいくつか例題にチャレンジしてみて計算出来るようになっておきましょう!
重要ポイント2. 掃き出し法の手順・簡約化の流れ・行列のランク
行列や連立方程式において重要になってくるのが掃き出し法。
連立方程式を解くときには掃き出し法は基本になってきます。
基本変形を使って連立一次方程式を解く方法を掃き出し法と言い、基本変形は以下の3つの変形を言う。
- 1つの式を何倍かする(ただし0倍は含まない)
- 2つの式を入れ替える
- 1つの式に他の式の何倍かを加える
では次の連立方程式を掃き出し法を使って解いてみましょう。
\[ \left\{\begin{align} 3x_1 + 2x_2 & = & 9 \\ 2x_1 + x_2 & = & 5 \end{align}\right. \]

掃き出し法を使って解くことが出来ました!
今の例では連立方程式のまま解きましたが、実は行列として表現して解くこともできるんです。
行列と連立方程式の関係についてはこちらの記事を参考にしてみてくださいね。
先ほどの連立方程式を行列で表現するとこのようになります。
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
3 & 2 & 9 \\
2 & 1 & 5 \\
\end{array}
\right]$$
この連立方程式を表した行列を拡大係数行列と言います。
これを先ほどの基本変形を使って変形していきましょう。

このように連立方程式の変形と行の変形が対応しているのが分かりますね。
そして変形された行列は左側が単位行列、右側が連立方程式の解になっていることが分かります。
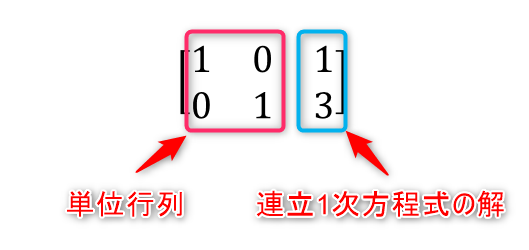
この行列を連立方程式に戻してみると、このように解が求まった形で式が出てきます。
\[ \left\{\begin{align} x_1& = & 1 \\ x_2 & = & 3 \end{align}\right. \]
このように連立方程式は拡大係数行列を用意して基本変形を使って単純な形に変形し、それに対応する連立方程式を考えることによって解くことが出来るというわけですね!
さて、続いては行列の簡約化。
簡約化とは行列をスッキリ簡単な形にすること。
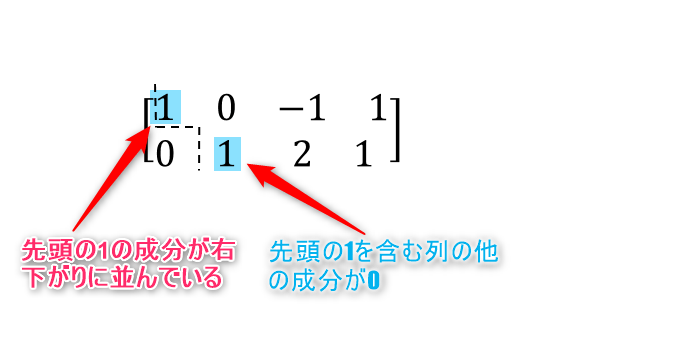
具体的に簡約な行列とは次のような行列のことを言います。
- 行の0以外の先頭の成分が1で、その成分を含む列の他の成分が0であるような行列
- 先頭の1の成分は右下がりに並んでいる
簡約化の手順は簡単で行列の基本変形を使うだけです。
- 1つの行を何倍かする(ただし0倍は含まない)
- 2つの行を入れ替える
- 1つの行に他の行の何倍かを加える
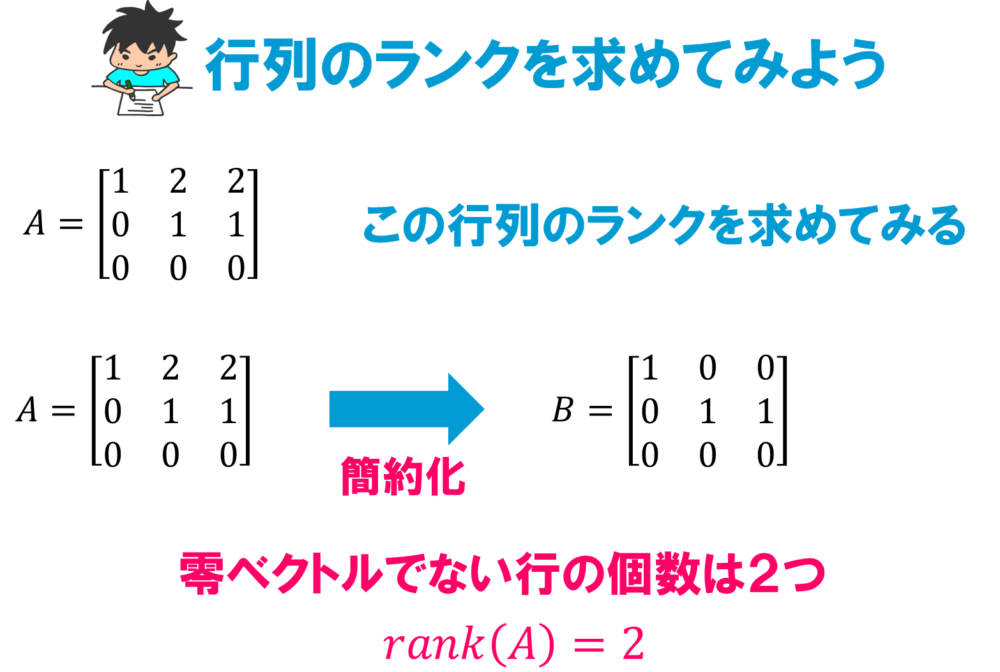
最後は行列のランク。
ランクは逆行列や1次独立などと深い関係があり、非常に重要な概念です。
行列のランクは簡約化を使えばすぐに求めることが可能。
ランクに関する詳しい解説はこちらの記事を参考にしてみてください。
重要ポイント3. 行列式の求め方
行列式は線形代数でもよく出てくるものですが、正方行列に対して定義される量と理解しておくと良いと思います。
計算方法としてはたすき掛けをイメージすると分かりやすいです。
では、こちらの行列の行列式を求めてみましょう。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
-1 & 2 \\
4 & -5 \\
\end{array}
\right]$$
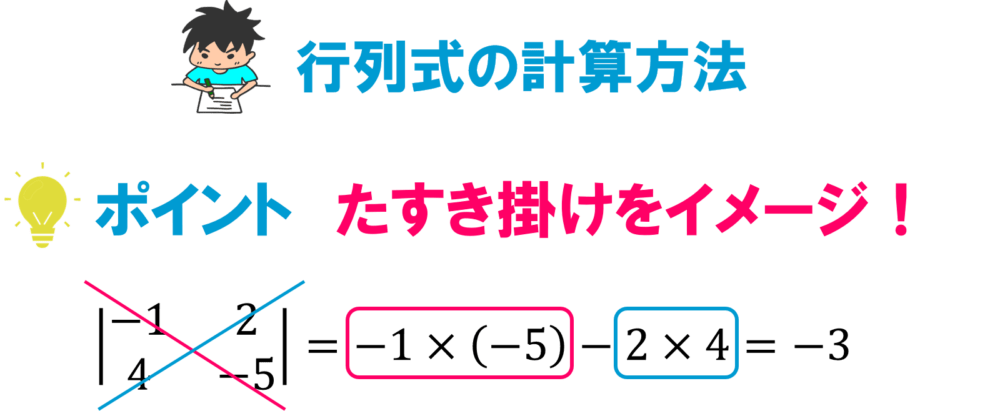
3×3行列も同様にたすき掛けをイメージしますが、こちらは少し複雑。
こちらの行列を例に見ていきましょう。
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 2 & 3 \\
4 & -2 & 1 \\
1 & 4 & 5
\end{array}
\right]$$
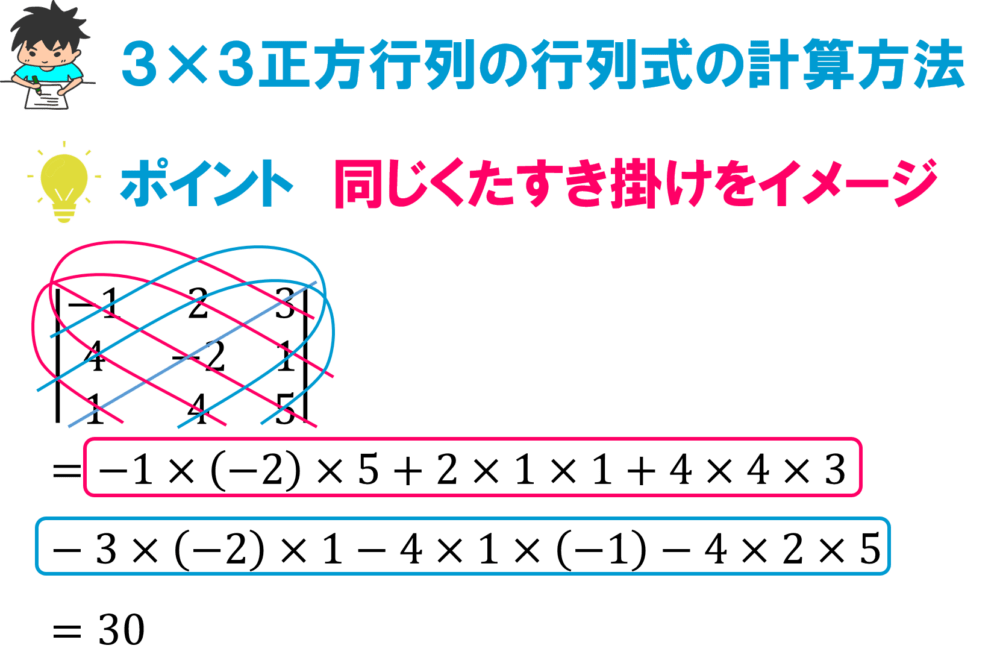
行列式は本当によく使うのでしっかり計算出来るようにしておきましょう!
行列式の図形的意味やさらに詳しい解説はこちらの記事に書いています。
重要ポイント4. 逆行列の求め方
逆行列を求めるには掃き出し法を使う方法と余因子を使う方法の2つがあります。
まずは掃き出し法を使った方法を解説します。
例えば次の行列の逆行列を求めてみましょう。
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
4 & 2 & 3 \\
2 & 1 & 1 \\
3 & 2 & 3 \\
\end{array}
\right]$$
まずは行列\(A\)の隣に単位行列を並べます。

ではこの単位行列を並べてできた行列を簡約化していきます。
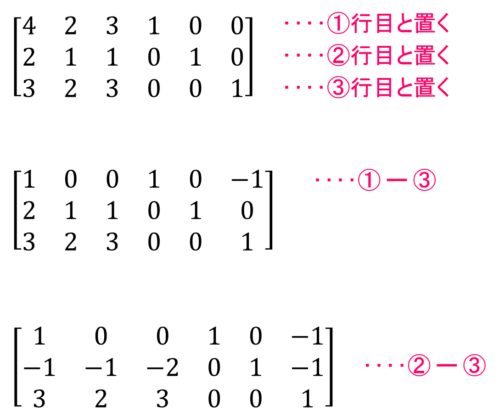

これで右側に現れた行列が逆行列になります。
$$\boldsymbol{A^{\mathrm{-1}}} = \left[
\begin{array}{rrr}
1 & 0 & -1 \\
-3 & 3 & 2 \\
1 & -2 & 0
\end{array}
\right]$$
では次に余因子行列を使って逆行列を求めてみます。
その際には余因子行列と行列式を使ったこちらの公式を用います。

では、例としてこちらの行列の逆行列を求めてみましょう。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
-1 & 2 \\
4 & -5 \\
\end{array}
\right]$$



検算で単位行列が出てきたということは正しい逆行列が求められたということですね!
重要ポイント5. 1次独立・1次従属・ベクトルの内積
1次独立、1次従属は線形代数においても重要な概念。
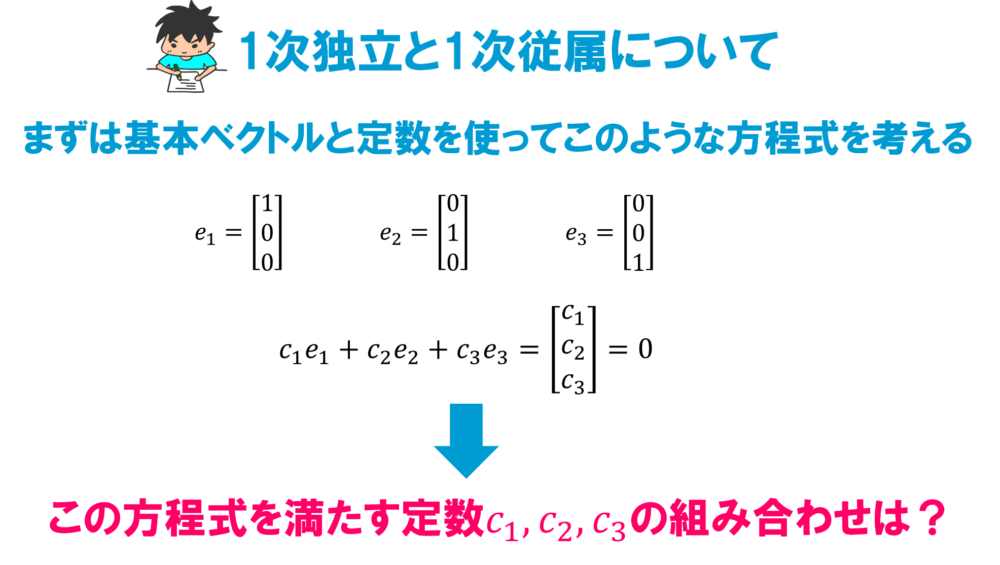
例えばこのような方程式を考えてみると、1次独立、1次従属は次のように定義されます。
\[c_1\textbf{u}_1+c_2\textbf{u}_2+c_3\textbf{u}_3=0\]
- 1次独立とは、上記の方程式を満たす\(c_1,c_2,c_3\)が\(c_1=c_2=c_3=0\)に限るとき\(\textbf{u}_1,\textbf{u}_2,\textbf{u}_3\)は1次独立であると言います。
- 1次従属とは、上記の方程式を満たす\(c_1,c_2,c_3\)が\(c_1=c_2=c_3=0\)意外に存在するとき\(\textbf{u}_1,\textbf{u}_2,\textbf{u}_3\)は1次従属であると言います。


1次従属についても見ていきます。
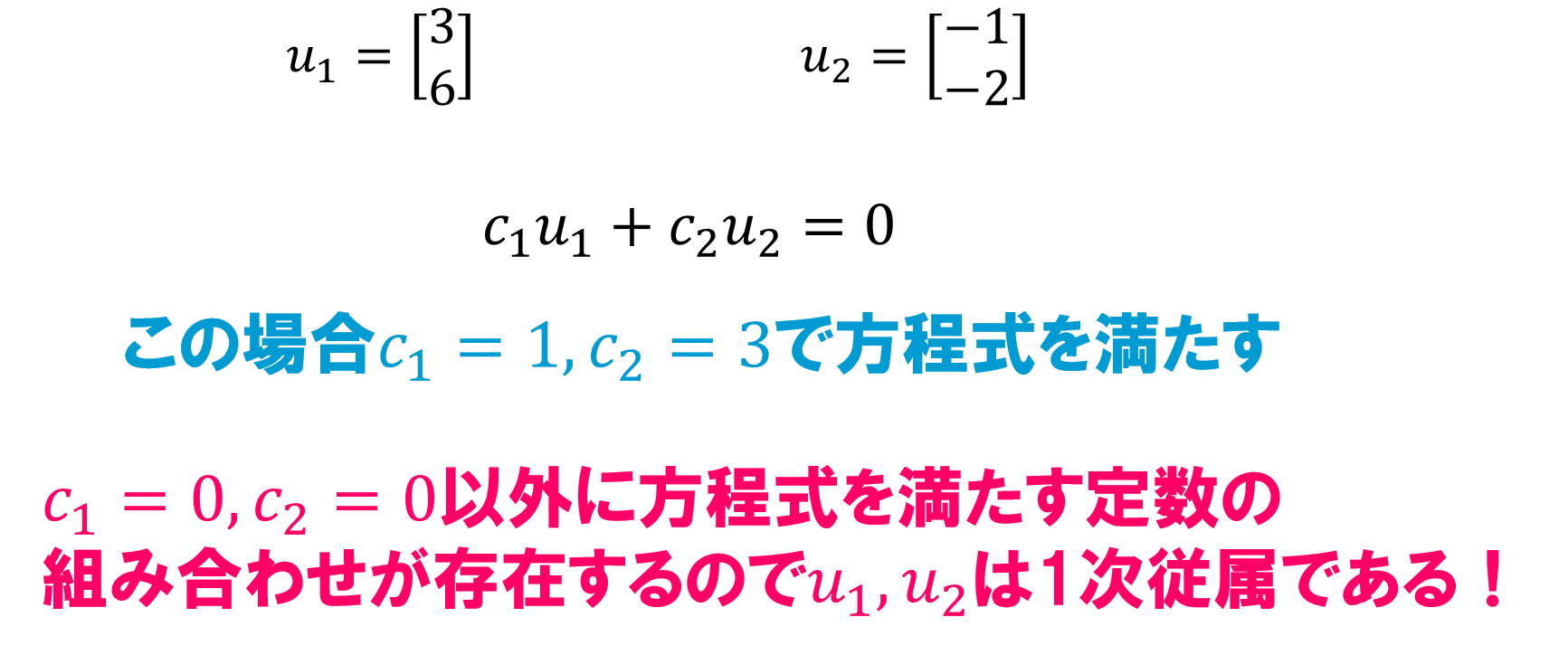
このように具体例を使えば分かりやすいですね。
続いてベクトルの内積ですが、高校の時に勉強した方も多いと思います。
高校での内積の定義はこのように表されるのでした。
大学生での線形代数の内積の定義を厳密に解説するとかなり複雑になるのですが、ここではよく出てくる標準内積について紹介します。
では実際に標準内積を計算してみましょう。

実質成分同士のかけ算をしているだけなのでそこまで難しくないことが分かりますね!
重要ポイント6. 固有値を求める手順
まず固有値と固有ベクトルが何なのかというところから確認しておきましょう。
- ベクトル\(x\)を行列\(A\)で線形変換した結果ベクトル\(x\)の定数倍になるとき、その定数を固有値、元のベクトル\(x\)を固有ベクトルという。(ただし\(x\)は0ベクトル以外)
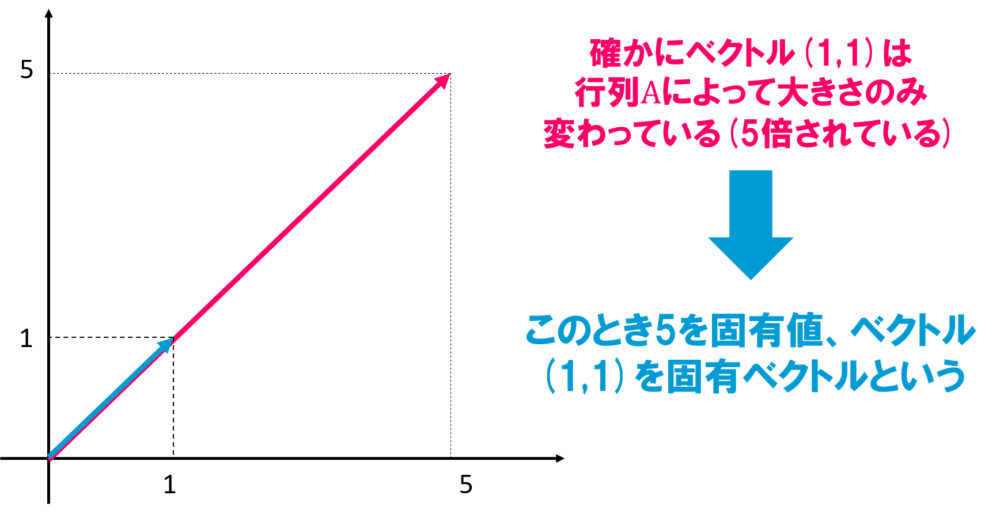
例えば以下のベクトルを行列\(A\)で線形変換してみることを考えます。
その結果元のベクトルの5倍のベクトルが出てきますが、この時の5を固有値、元のベクトル\(x\)を固有ベクトルというわけですね。
$$\boldsymbol{x} = \left[ \begin{array}{r} 1\\ 1 \\ \end{array} \right],\boldsymbol{A} = \left[ \begin{array}{rr} 3 & 2 \\ 4 & 1 \\ \end{array} \right]$$
$$\boldsymbol{A}\boldsymbol{x} = \left[ \begin{array}{rr} 3 & 2 \\ 4 & 1 \\ \end{array} \right]\left[ \begin{array}{rr} 1 \\ 1 \\ \end{array} \right] = 5\left[ \begin{array}{rr} 1\\ 1 \\ \end{array} \right]$$
図解してみるとこのようになります。
ベクトルは回転せずに大きさだけ変わっているということが分かりますね。
では実際に固有値を求めてみましょう。
固有値を求めるにはこちらの公式を用います。
\[|λE-A|=0\]
この公式がどのように求まるのかということについてはこちらの記事に詳しく書いているので参考にしてみてください。
今回はこの行列の固有値を求めてみます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
3 & 2 \\
4 & 1 \\
\end{array}
\right]$$

答えを見てみると初めの例で出てきた5という固有値が求まっていることが分かりますね!
重要ポイント7. 対角化の手順
対角化と聞くとなんだか難しそうですがやっていることは至って単純。


対角化をするにはこの3つのステップを踏むだけ。
- 行列\(A\)の固有ベクトルを並べた行列\(P\)を作る
- 逆行列\(P^{\mathrm{-1}}\)を求める
- \(P^{\mathrm{-1}}AP\)を求める
では実際に計算してみましょう。
今回はこちらの行列を対角化してみます。
$$\boldsymbol{A} = \left[ \begin{array}{rr} 2 & -2 \\ -1 & 3 \\ \end{array} \right]$$




これで対角化することが出来ました!
対角行列を見てみると行列\(A\)の固有値が対角成分になっていること分かります。
これは対角化の検算としても使える面白い性質なので覚えておくと便利ですね!












