

さて、今回はベクトルの1次独立と1次従属についてです。
少し聞き慣れない言葉かもしれませんが、ベクトルの足し算やかけ算を使ったあまり難しい内容ではないので安心してください。
ではさっそく学んでいきましょう!
1次結合って何?
1次独立と1次従属の前にまずは1次結合について見ておきましょう。
1次結合とは、一つのベクトルを他のベクトルの組み合わせで表すことを言います。
例えば次のベクトル\(\textbf{a}\)をベクトル\(\textbf{b}\)と\(\textbf{c}\)を使って表してみます。
$$\boldsymbol{a} = \left[
\begin{array}{r}
5\\
8 \\
\end{array}
\right]\boldsymbol{b} = \left[
\begin{array}{r}
3\\
4 \\
\end{array}
\right]\boldsymbol{c} = \left[
\begin{array}{r}
-1\\
-1 \\
\end{array}
\right]$$

ベクトル\(\textbf{b}\)を3倍、ベクトル\(\textbf{c}\)を4倍して足してみるとちょうどベクトル\(\textbf{a}\)になりますね。
$$\boldsymbol{a} = \left[
\begin{array}{r}
5\\
8 \\
\end{array}
\right]= 3\left[
\begin{array}{r}
3\\
4 \\
\end{array}
\right]+4\left[
\begin{array}{r}
-1\\
-1 \\
\end{array}
\right]$$
このようにベクトル\(\textbf{a}\)がベクトル\(\textbf{b}\)と\(\textbf{c}\)の定数倍の和で書けるとき、ベクトル\(\textbf{a}\)は\(\textbf{b}\)、\(\textbf{c}\)の1次結合で書けると言います。
ではもう一つ例を見てみましょう。
同じように,以下の\(\textbf{a}\)というベクトルををベクトル\(\textbf{e}_1\)と\(\textbf{e}_2\)を使って表してみます。
$$\boldsymbol{a} = \left[
\begin{array}{r}
5\\
8 \\
\end{array},
\right]\boldsymbol{e_1} = \left[
\begin{array}{r}
1\\
0 \\
\end{array},
\right]\boldsymbol{e_2} = \left[
\begin{array}{r}
0\\
1 \\
\end{array}
\right]$$
これはこのように簡単に1次結合で表すことが出来ますね!
$$\boldsymbol{a} = \left[
\begin{array}{r}
5\\
8 \\
\end{array}
\right]= 5\left[
\begin{array}{r}
1\\
0 \\
\end{array}
\right]+8\left[
\begin{array}{r}
0\\
1 \\
\end{array}
\right]$$
これで1次結合については完璧です。
では、この内容を踏まえて1次独立と1次従属について学んでいきましょう!
1次独立・1次従属って?
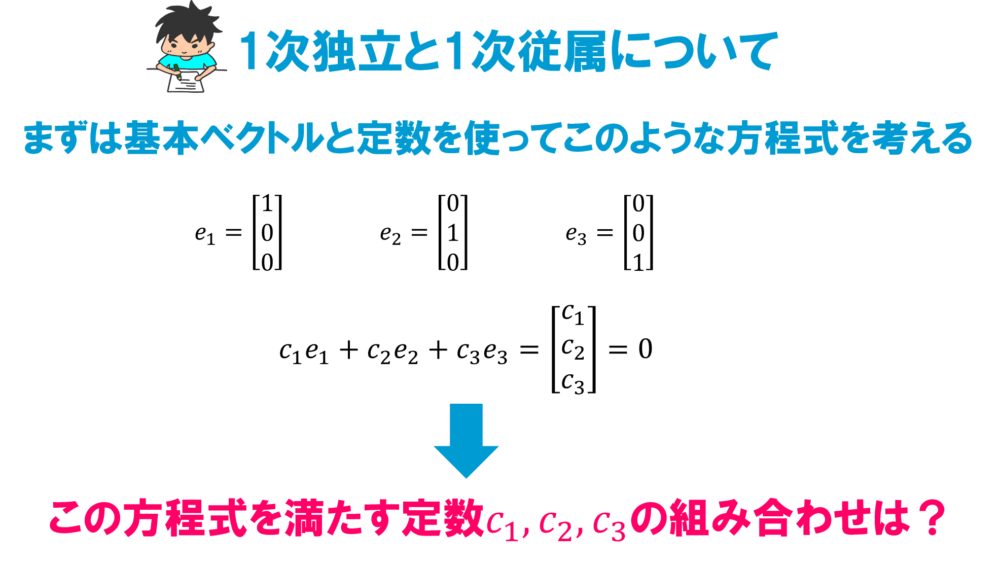
1次独立と1次従属について考えるために、まずこのような方程式を用意します。
\[c_1\textbf{u}_1+c_2\textbf{u}_2+c_3\textbf{u}_3=0\]
\(c_1,c_2,c_3\)は定数で、\(\textbf{u}_1,\textbf{u}_2,\textbf{u}_3\)は同じ型を持つベクトルです。
ではまずは1次独立と1次従属の定義から見ておきましょう。
- 1次独立とは、上の方程式を満たす\(c_1,c_2,c_3\)が\(c_1=0,c_2=0,c_3=0\)に限るとき\(\textbf{u}_1,\textbf{u}_2,\textbf{u}_3\)は1次独立であると言います。
- 1次従属とは、上の方程式を満たす\(c_1,c_2,c_3\)が\(c_1=0,c_2=0,c_3=0\)以外に存在するとき\(\textbf{u}_1,\textbf{u}_2,\textbf{u}_3\)は1次従属であると言います。



では1次従属の例も見てみましょう。
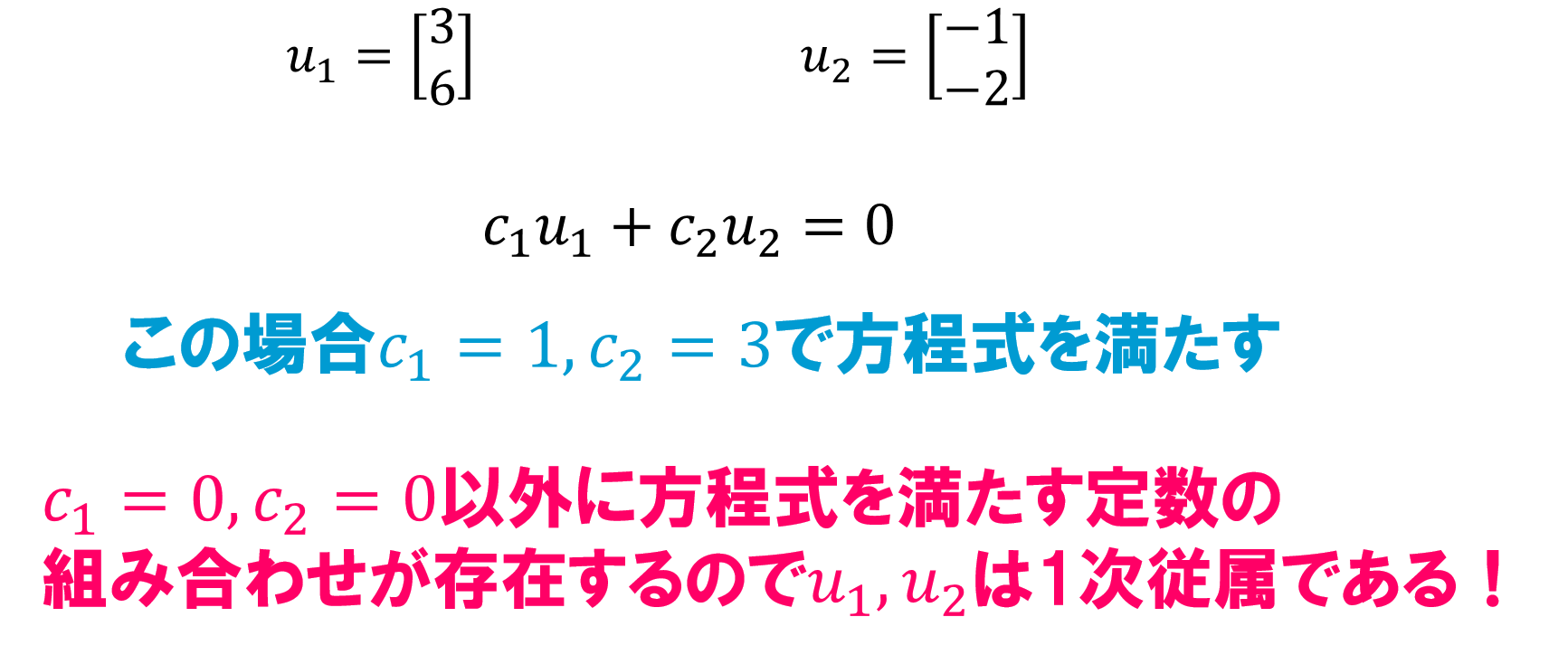
これで1次独立と1次従属のイメージはなんとなく掴めたでしょうか?

では、次は簡約化を使ってベクトルが1次独立か1次従属かを調べてみましょう!
簡約化を使って調べてみよう
今回はこちらのベクトルたちが1次独立か1次従属かを調べてみます。
$$\boldsymbol{a_1} = \left[
\begin{array}{r}
2\\
0\\
0\\
2 \\
\end{array}
\right]\boldsymbol{a_2} = \left[
\begin{array}{r}
2\\
3\\
3\\
2 \\
\end{array}
\right]\boldsymbol{a_3} = \left[
\begin{array}{r}
0\\
3\\
4\\
3 \\
\end{array}
\right]$$
1次独立か1次従属かを調べる手順は至って簡単。
まずはこのように方程式を準備します。
\[c_1\textbf{a}_1+c_2\textbf{a}_2+c_3\textbf{a}_3=0\]
あとはこの方程式を\(c_1,c_2,c_3\)について解いて、\(c_1,c_2,c_3\)の解が全て0になるか、0以外の答えになるかを調べるだけ。
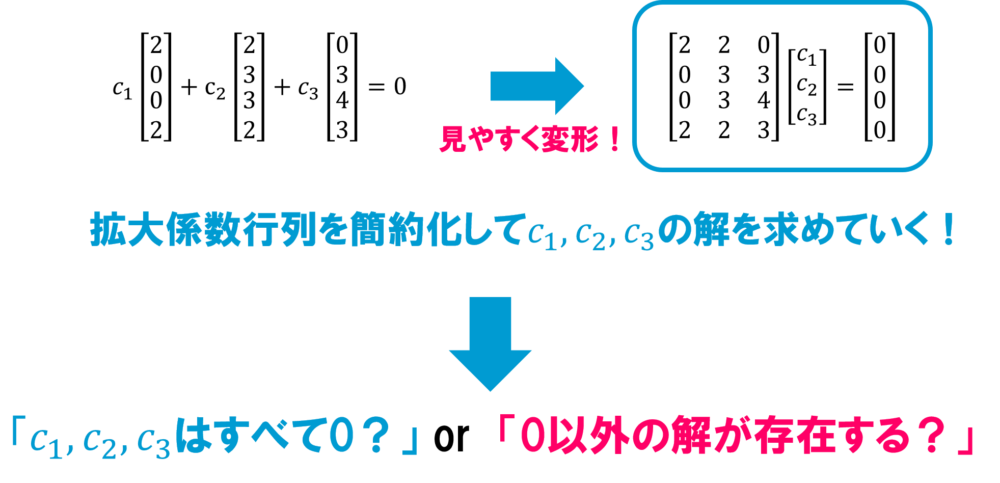
この際に方程式を解くときに簡約化を使うということですね。
ではさっそく解いてみましょう!

よってこの拡大係数行列に対応する方程式を考えると、、、


このように1次独立か1次従属かを調べる手順はとてもシンプルで、拡大係数行列と簡約化という今まで学んできた知識を使うだけ。
しっかりマスターしておきましょう!
まとめ: 大事な概念なので覚えておこう
さて、今回はベクトルの1次独立と1次従属について学んできました。
- 1次結合とは一つのベクトルを他のベクトルの組み合わせで表すこと
- 1次独立と1次従属は方程式を満たす定数が全て0かどうかの違い
- 簡約化を使って1次独立か1次従属かを調べることができる
今回勉強してきた内容は今後も登場してくるし、とても重要な内容なのでしっかり理解するようにしておいてください!













