線形代数における基底ってなに？

今回は基底というものについて解説していくよ！

聞いたこと無いけど、どんな内容なんだろう？

今回は基底について解説していきます。

少し複雑な概念かもしれませんが、まず最初に基底の概念について、そして次に具体例を使いながら分かりやすく解説していくので安心してついてきてください。

では早速学んでいきましょう！

基底とはなに？

基底に関しては参考書を見てみてもよくわからない書き方をされていることが多いんですよね。

なんとなく言っていることはわかるけど概念的にイメージできないというか。

なのでここではみなさんがイメージしやすいように噛み砕いた表現を使って説明していきます。

線形代数における基底(基とも言う)はこのような理解をしていただければオーケーです。

\(x,y\)軸みたいな感じ？

イメージ的にはそんな感じ！

あとで具体例を使って解説するので今は「こんなもんなんだな」くらいの理解で大丈夫です！

では次に基底と深い関係にあるベクトル空間というものについて見ていきます。

ベクトル空間とはなんなのか？

ベクトル空間についても参考書ではわかりにくい書き方がされていますね。。

しかし実際はもっと噛み砕いたこのような理解で良いと思います。

先程出てきた\(x,y\)軸が基底だとすればベクトル空間は軸によって構成される\(x,y\)平面ということになります。

これだけでは少しわかりにくいと思うので具体例を使って理解を深めていきましょう！

基底とベクトル空間の具体例をみていこう！

具体例を見ていけば基底とベクトル空間はそこまで難しくないものだということに気づいてもらえると思います。

まず基底とは座標系を作り出す1次独立なベクトルの集まりであると言いました。

ここでは次の2つのベクトルを基底として取ってみましょう。

$$\boldsymbol{\textbf{e}_1} = \left[
\begin{array}{r}
1\\
0 \\
\end{array}
\right],\boldsymbol{\textbf{e}_2} = \left[
\begin{array}{r}
0\\
1 \\
\end{array}
\right]$$

これらのベクトルは基本ベクトルですが、2つは互いに1次独立であるということは以前の記事で勉強しましたね。

そして内積が0になることから互いに直行していることが分かります。

つまりこの2つの基本ベクトルはこのように図示することが出来ます。

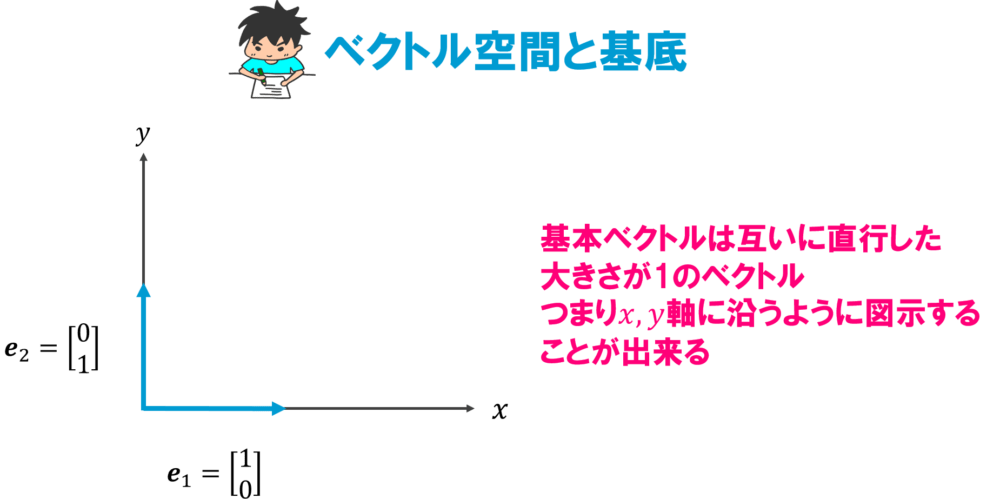
この図を見てみると、基本ベクトル\(\textbf{e}_1,\textbf{e}_2\)が\(x,y\)軸に相当し、\(x,y\)平面は基本ベクトルによって構成されていると言うことが出来ます。

つまり\(x,y\)平面というベクトル空間が基本ベクトル\(\textbf{e}_1,\textbf{e}_2\)という2つの基底によって構成されているということ。

これが基底とベクトル空間の関係です。

なんとなくわかってきた！

そしてベクトル空間に基底が与えられれば、その空間の座標は基底の線形結合(ベクトルの定数倍と和)によってただ一通りに表すことが出来ます。

また、基底の数をそのベクトル空間の次元と言います。

実際先程の座標系は\(x,y\)平面という2次元の座標系ですが、基底が2つであることから基底の数が次元に等しいことが分かりますね。

今は2次元の場合で解説していますが3次元、4次元と次元が増えても考え方は同じです。

まとめ: ややこしい概念は具体例で理解！

さて、今回は基底とベクトル空間というものについてかなり噛み砕いて解説してきました。

あまり分かりやすい解説のされた参考書が無いので概念を理解するのに苦しむかもしれませんが、ひとまずは今回のような理解で大丈夫です。

より厳密な解説は参考書に譲るとして、まずはイメージをしっかり掴んで理解するということを心がけましょう！