

行列のかけ算は少し特徴的です。
慣れるまでは少し手間取るかもしれませんが、慣れれば簡単。
分かりやすく解説していくので、頑張って学んでいきましょう!
行列のスカラー倍
まずは行列のスカラー倍から見ていきましょう。
行列のスカラー倍はいたって簡単。
行列の各成分をスカラー倍するだけです。

では次に行列と行列のかけ算を見ていきましょう。
行列と行列の掛け算のやり方

例として行列\(A\)と行列\(B\)のかけ算を考えます。
まず初めに注意しておかないといけないのは、行列\(A\)と行列\(B\)のかけ算は\(A\)の列の個数と\(B\)の行の個数が等しい場合でないと定義できないということ。
例えば行列\(A\)が2×3行列、行列\(B\)が3×2行列の場合は\(A\)の列の個数3と\(B\)の行の個数3が等しいのでかけ算できるということですね。
では行列\(A\)と行列\(B\)が以下のような場合、\(A\)と\(B\)の積\(A\)\(B\)をどのように計算していけばいいか見ていきましょう!
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 2 & 3 \\
4 & -5 & 6 \\
\end{array}
\right]$$
$$\boldsymbol{B} = \left[
\begin{array}{rrr}
-1 & 2 \\
4 & 3 \\
1 & 5
\end{array}
\right]$$
まずは\(A\)の1行目、\(B\)の1列目について計算します。
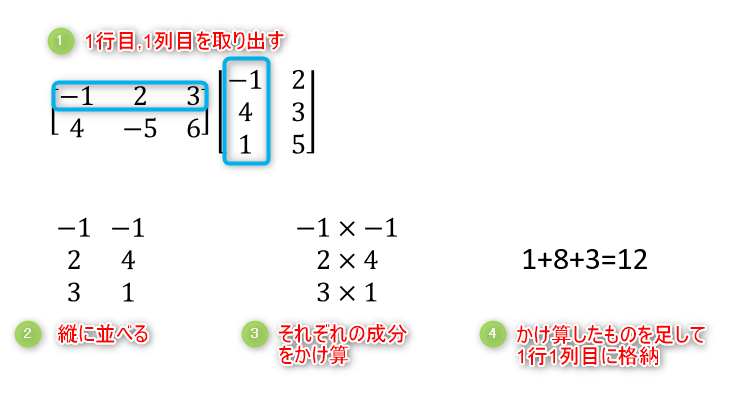
これで\(A\)\(B\)の1行1列目の成分の計算は完了です。
次に\(A\)の1行目、\(B\)の2列目について計算していきます。

これで\(A\)\(B\)の1行2列目の成分の計算は完了です。
この操作を2行1列目、2行2列目も同様に行います。
そして最終的な計算結果を以下のようになります。
$$\boldsymbol{AB} = \left[
\begin{array}{rrr}
-1 & 2 & 3\\
4 & -5 & 6 \\
\end{array}
\right]
\left[
\begin{array}{rr}
-1 & 2 \\
4 & 3 \\
1 & 5 \\
\end{array}
\right]
= \left[
\begin{array}{rr}
12 & 19 \\
-18 & 23 \\
\end{array}
\right]
$$

計算結果を見てみると分かりますが、\(A\)\(B\)が2×2行列になっています。
一般に\(A\)が\(m\)×\(n\)行列、\(B\)が\(n\)×\(r\)行列の時、\(A\)\(B\)は\(m\)×\(r\)行列になるので覚えておきましょう!
具体例を使った実際の計算


例えば次のような例を考えてみましょう。
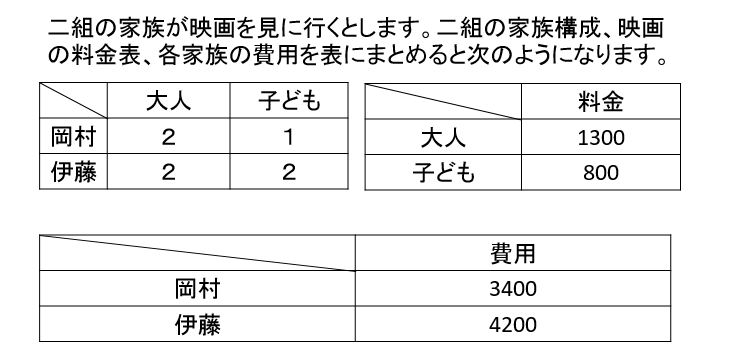
これを行列計算に置き換えてみます。
行列\(A\)と行列\(B\)を以下のように定義し、積\(A\)\(B\)を計算してみましょう。
$$\boldsymbol{A} = \left[ \begin{array}{rr} 2 & 1 \\ 2 & 2 \\ \end{array} \right]$$
$$\boldsymbol{B} = \left[ \begin{array}{rr} 1300 \\ 800 \\ \end{array} \right]$$
先ほど示した計算例のように計算してみると、積\(A\)\(B\)は以下のようになります。
$$\boldsymbol{AB} = \left[ \begin{array}{rr} 3400 \\ 4200 \\ \end{array} \right]$$

このように具体例を使って見ていくと行列のかけ算方法にも納得がいくのではないでしょうか?
まとめ:ややこしく見えるが慣れれば簡単
さて、今回は行列のかけ算について見てきました!
少し複雑に見えたかけ算も具体例を通して計算してみると意外と簡単だったのではないでしょうか?
もう一度内容をまとめておきましょう。
- スカラー倍‥‥行列の各成分をスカラー倍するだけ。
- 行列と行列のかけ算‥‥\(A\)の行、\(B\)の列を取り出して成分同士をかけ算して足す。そして対応する場所に値を格納。
練習のために参考書の問題を解くなどして行列のかけ算をしっかりマスターしておきましょう!













