

前回、逆行列の基本的な性質について見てきました。
その際は逆行列は存在するものとして話を進めてきました。
しかし実は必ずしも逆行列は存在するわけでは無いんです。
今回はそんな逆行列が存在しない場合について見ていきましょう!
点に行列をかけてみよう
逆行列が存在しないことをイメージ的に理解するために「点の移動」を考えてみましょう。
今回は点\((1,1)\)に行列\(A\)をかけた時にどのような点の移動をするか見てみます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
2 & 1 \\
3 & 2 \\
\end{array}
\right]$$
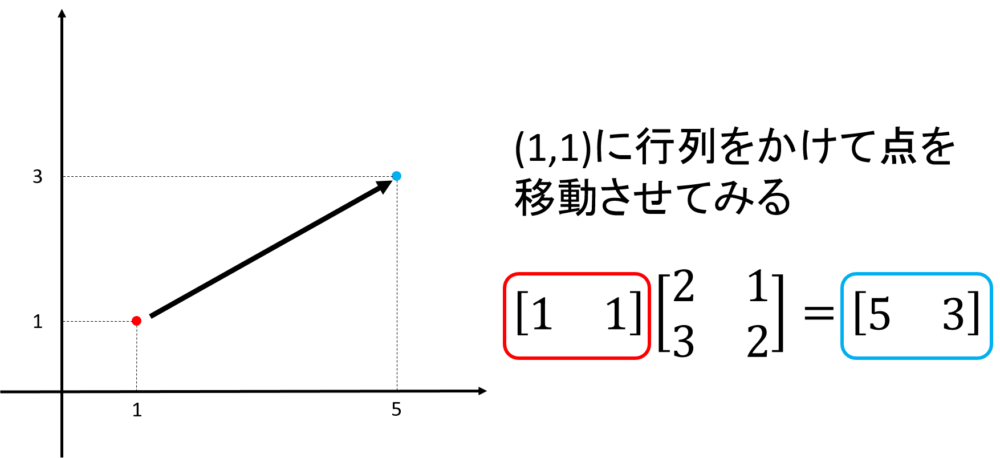

ではこの移動した点\((5,3)\)に行列\(A\)の逆行列をかけた時に点がどのように移動するか見てみてましょう!
逆行列をかけると元の場所に戻った
では行列\(A\)の逆行列\(A^{\mathrm{-1}}\)を点\((5,3)\)にかけてみます。
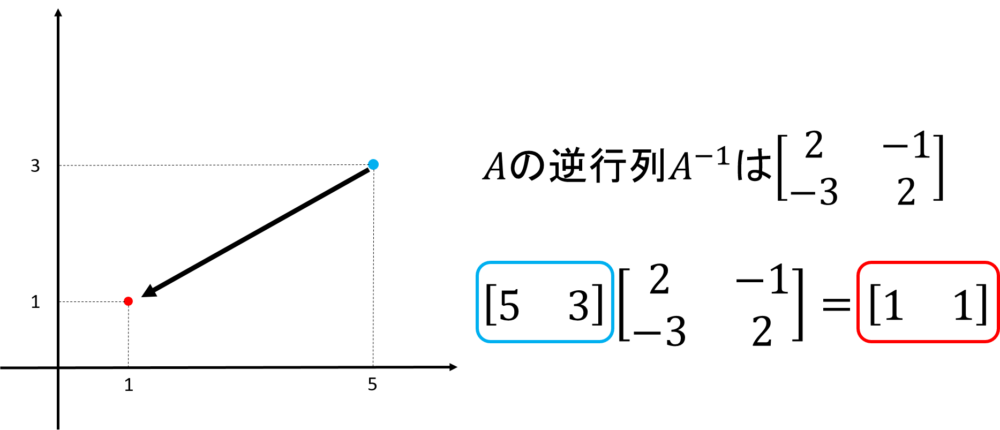

このように逆行列が存在するときは座標を元の位置に戻すことが出来るんです。
逆行列がないときもある
では、逆行列が存在しない時はどうなるでしょうか?
先ほどの点の移動に例えると逆行列が存在しない時には移動してしまった点を元の位置に戻すことが出来ないということに対応します。
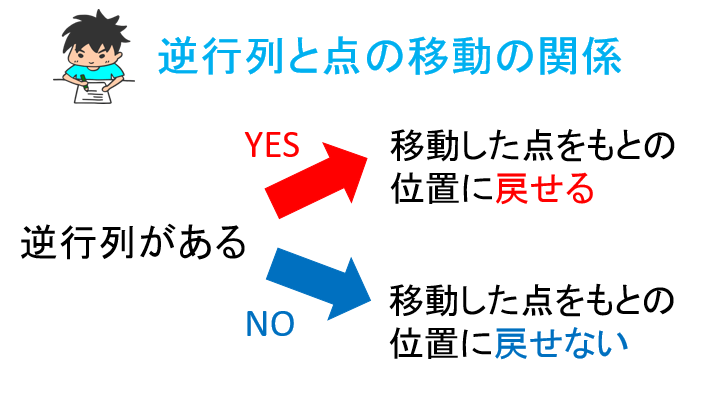
このようにグラフで理解してみると逆行列が存在しないイメージもつかみやすいですね!
まとめ:「変換」に例えるとわかりやすい
さて、今回は逆行列が存在しない場合をグラフを使いながら見てきました。
逆行列の求め方も大事ですが、まずは逆行列がどのようなものなのかイメージ出来ることが大事。
逆行列は線形代数でも大事な内容なのでしっかり理解しておきましょう!













