

さて、今回は固有値と固有ベクトルについて見ていきます。
大学の線形代数でも終盤に学ぶ内容ですが、実はそこまで難しい内容ではないんです。
図解的な理解の仕方も解説していくのでしっかり理解していきましょう!
固有値,固有ベクトルってなに?
以前の記事で線形写像について解説してきました。
そして、線形写像とは1変数同士または多変数同士を対応付けることでしたね。
その知識を踏まえて次のような線形変換を考えてみます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
1 & 2 \\
-2 & 3 \\
\end{array}
\right],y=Ax$$
ただし\(x,y\)はそれぞれこのような列ベクトルとします。
$$\boldsymbol{x} = \left[
\begin{array}{r}
x_1\\
x_2 \\
\end{array}
\right],\boldsymbol{y} = \left[
\begin{array}{r}
y_1\\
y_2 \\
\end{array}
\right]$$
この\(Ax\)を展開するとこのようになりますね。
$$Ax = \left[
\begin{array}{rr}
1 & 2 \\
-2 & 3 \\
\end{array}
\right]\left[
\begin{array}{r}
x_1\\
x_2 \\
\end{array}
\right]=\left[
\begin{array}{r}
x_1+2x_2\\
-2x_1+3x_2 \\
\end{array}
\right]$$
この\(x_1,x_2\)に\(x_1=1,x_2=1\)を代入してみます。
$$Ax = \left[
\begin{array}{rr}
1 & 2 \\
-2 & 3 \\
\end{array}
\right]\left[
\begin{array}{r}
1\\
1 \\
\end{array}
\right]=\left[
\begin{array}{r}
1+2\\
-2+3 \\
\end{array}
\right]=\left[
\begin{array}{r}
3\\
1 \\
\end{array}
\right]$$

では変換する前のベクトルと変換したあとのベクトルを図示してみます。
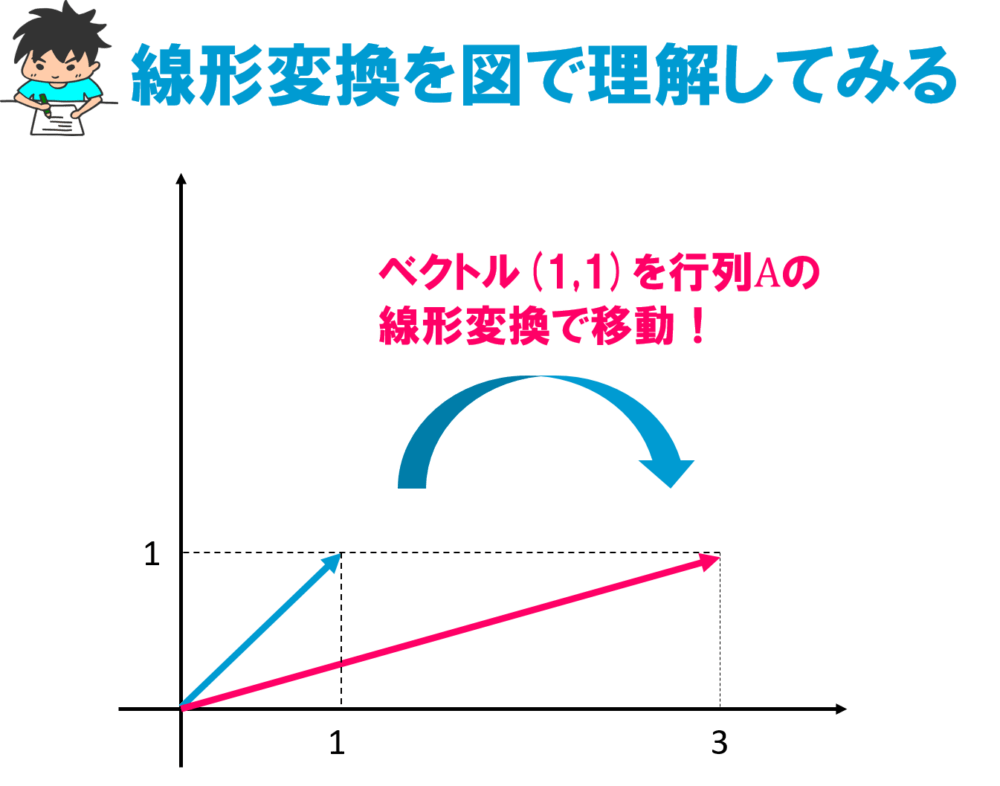
線形変換によってベクトルが回転し、長さも拡大していることがよくわかりますね。
このように線形写像は「ベクトルを回転し拡大または縮小させること」と言うこともできるんです。

これが線形写像の図形的な理解です。
では、ここで1つ特殊な場合を考えてみます。
「もしベクトルに行列をかけて、回転させずに大きさのみを変えることが出来たら?」
例えば次の行列の線形変換を考えてみます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
3 & 2 \\
4 & 1 \\
\end{array}
\right],y=Ax$$
ここに\(x_1=1,x_2=1\)を代入して線形変換してみると、
$$Ax = \left[
\begin{array}{rr}
3 & 2 \\
4 & 1 \\
\end{array}
\right]\left[
\begin{array}{r}
1\\
1 \\
\end{array}
\right]=\left[
\begin{array}{r}
3+2\\
4+1 \\
\end{array}
\right]=\left[
\begin{array}{r}
5\\
5 \\
\end{array}
\right]=5\left[
\begin{array}{r}
1\\
1 \\
\end{array}
\right]$$

実はこれが固有値と固有ベクトルなんです!
つまり、ある行列\(A\)にベクトル\(x\)をかけた結果としてその定数倍になる場合,そのベクトル\(x\)を固有ベクトル,定数倍の値を固有値と呼ぶということ。
今の例では5が固有値でベクトル(1,1)が固有ベクトルということになります。
これを図で見てみると確かにベクトルが回転せずに大きさのみ変わっている(定数倍されている)ということがわかりますね!
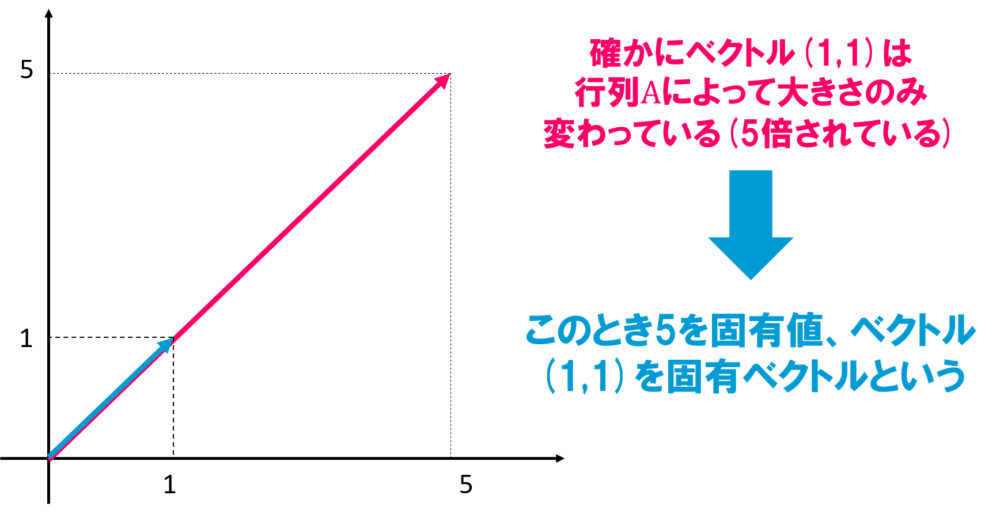
- 行列\(A\)で線形変換してもベクトル\(x\)は回転せず、大きさのみ変わっている
- このときの定数倍の値を固有値、元のベクトル\(x\)を固有ベクトルと呼ぶ(ただし\(x\)は0ベクトル以外)
固有値を求めてみよう!
ではここからは実際に固有値を求めてみましょう。
先ほどの固有値の意味から、固有値を\(λ\)とするとこのような等式が成り立つことはわかりますか?
\[Ax=λx\]
ベクトル\(x\)に行列\(A\)をかけるともとのベクトルの固有値倍になるということですね。
この等式を\(λ\)について解くことができれば固有値を求めることが出来ます。
この等式を変形してみると、、、

ここまで落とし込むことが出来ました!
では\(λE-A\)に逆行列が存在しないという条件をどのように表現すればいいでしょうか?
ここで以前勉強した逆行列を余因子行列と行列式で求める公式を思い出してみてください。
このような公式で与えられるのでした。

この式を見てみると分母に行列式がありますね。
つまりこの行列式が0でない場合に逆行列が存在するということ。
ということは行列式が0ならば逆行列は存在しないことになります。


これが固有値を求めるための公式になります。
では具体的に固有値を求めてみましょう!
今回はこの行列\(A\)の固有値を求めてみます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
3 & 2 \\
4 & 1 \\
\end{array}
\right]$$

これで固有値が求まりました!
始めの例で出てきた固有値5が確かに求まっていますね。
では最後にこれらの固有値に対応する固有ベクトルを求めてみましょう!
固有ベクトルを求めてみよう
固有値が\(λ=-1,5\)と2つの値を取るので場合分けして考えます。
固有ベクトルを求めるには先ほどのこの式に固有値を代入して\(x\)について解くことによって求まります。
以下の式に固有値を代入して\(x\)について解く。
\[(λE-A)x=0\]
λ=5の場合
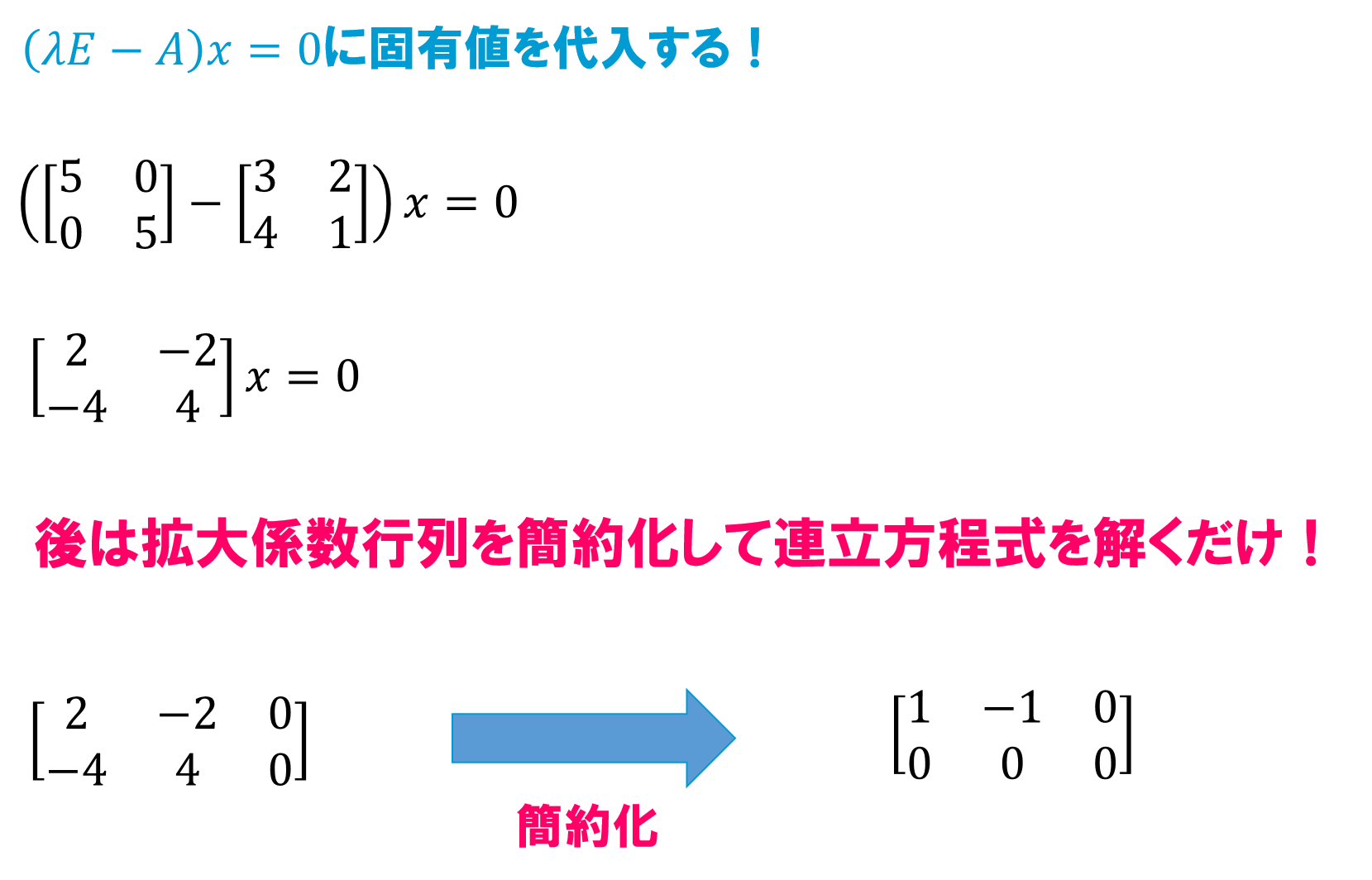


始めの例で出てきた固有ベクトルは\(c=1\)の場合に対応していることが確認出来ますね。
ではもう一つの固有値についても固有ベクトルを求めてみましょう。
λ=ー1の場合


これで2つの固有値に対する固有ベクトルが求まりました!
このプロセスをしっかり理解しておきましょう!
まとめ: 具体例で見てみると簡単
さて、今回は固有値と固有ベクトルについて具体例をたくさん使いながら見てきました。
今回の内容をもう一度振り返っておきましょう!
- ある行列\(A\)において、その行列にベクトル\(x\)をかけた結果としてその定数倍になる場合,そのベクトル\(x\)を固有ベクトル、その値を固有値と呼ぶ。(ただし、xは0ベクトル以外)
- 固有値は行列式\(|λE-A|\)=0を解くことで求める。
- 固有ベクトルは固有値を代入した\((λE-A)x=0\)を\(x\)について解く。
かなりボリューミーな内容になりましたが、内容をしっかり押さえながら理解していきましょう!













