

ベクトルについては高校でも学んできました。
今回はそのベクトルについて行列の内容に絡めて学んでいきます。
ではさっそくいきましょう!
高校でも習ったベクトルの基礎
まずは高校で習ったベクトルの復習から。
以前の記事でベクトルは行列の1種であると説明しました。
例えば次の行列は2行1列の行列ですが、2次の列ベクトルと言います。
$$\boldsymbol{u} = \left[
\begin{array}{r}
-1\\
4 \\
\end{array}
\right]$$
こちらは1行3列の行列ですが、3次の行ベクトルと言うわけですね。
$$\boldsymbol{v} = \left[
\begin{array}{rrr}
-1 & 20 & 3 \\
\end{array}
\right]$$
このような列ベクトルや行ベクトルをあわせて数ベクトルと言います。
また、すべての成分が0の数ベクトルを零ベクトルと言うのでこちらも合わせて覚えておきましょう。

ベクトルの足し算・引き算も行列と同じように考えることが出来ます。
例えば次の2つのベクトルを足し算・引き算してみましょう。
$$\boldsymbol{u} = \left[
\begin{array}{r}
-1\\
4 \\
\end{array}
\right]\boldsymbol{v} = \left[
\begin{array}{r}
2\\
1 \\
\end{array}
\right]$$

計算過程は至ってシンプルですね!
では次に高校でも習った内積について行列を使いながら考えていきます。
内積を行列のかけ算で表そう
高校で習った内積は覚えていますか?
次のような定義でしたね。
\(|\textbf{a}|\),\(|\textbf{b}|\)はそれぞれのベクトルの大きさ、\(θ\)は2つのベクトルがなす角です。
では行列で定義するとどうなるでしょうか?
厳密に言えば内積の定義には条件がいくつかあるのですが、今回は標準内積を紹介します。
\(\textbf{a}\)と\(\textbf{b}\)が同じ型の列ベクトルのとき、標準内積は次のように定義されます。
少し複雑に感じるかもしれませんが、具体例を見てみればスムーズに理解出来るはず。

ベクトルの内積も行列のかけ算に落とし込むことができるので特に難しいところは無いかなと思います。
大学では要素数が4を越えることも
さて、高校ではベクトルというと2次元や3次元のものを扱ってきましたよね。
つまりベクトルの要素数が2つや3つということに対応します。
しかし大学ではさらに成分の数が増えて、要素数が4つや5つになることもあるんです。
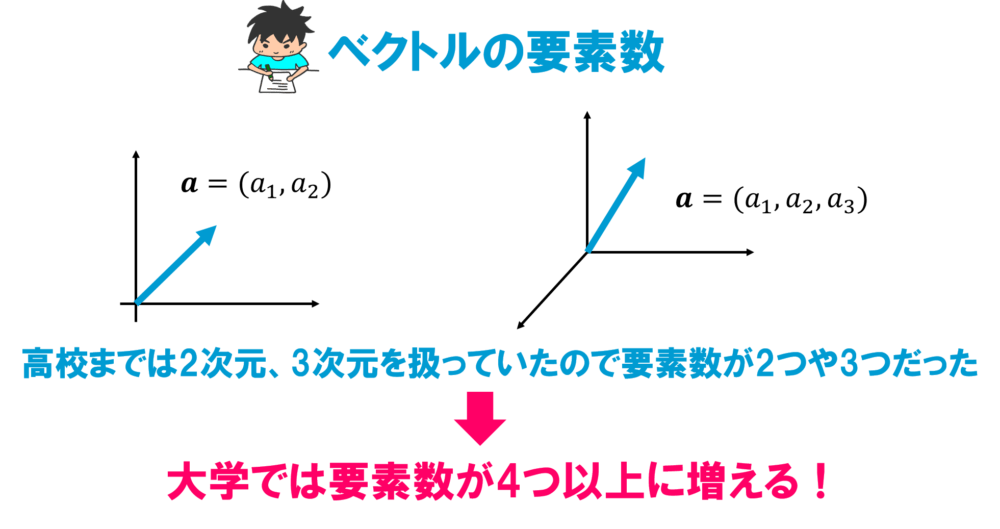
要素数が増えることで図形的な対応は考えづらくなりますが、今はとりあえず「要素数が増えたベクトルを扱っていくんだな」くらいに考えておいてください!
まとめ: 線形代数では行列は頻出!
さて、今回はベクトルについて行列の内容と絡めて見てきました。
線形代数ではベクトルも行列の一種として扱うため、やはり行列の知識が重要になってきます。
これまで学んできた内容が引き続き大切になってくるということですね。
これからベクトルについて学んでいきますが、今までの内容の延長線上にあるんだということをしっかり意識しながら学んでいきましょう!













