

前回の記事で1次独立と1次従属について解説してきました。
今回は行列のランクについて見ていきます。
また、前回の1次独立とランクの関係についても見ていくので頑張っていきましょう!
行列のランクってなんなの?
ではまず行列のランクがどのようなものなのか、というところから押さえていきましょう。
例えば次の簡約化された行列は零ベクトルでない行の個数が3つなのでランクが3ということ。
$$\boldsymbol{B} = \left[
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right] , rank(B)=3$$
また、この簡約化された行列は零ベクトルでない行の個数が2つなのでランクは2ということになります。
$$\boldsymbol{C} = \left[
\begin{array}{rrr}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0
\end{array}
\right] , rank(C)=2$$
では、実際に行列が与えられたときにその行列のランクを簡約化を使って求めてみましょう。
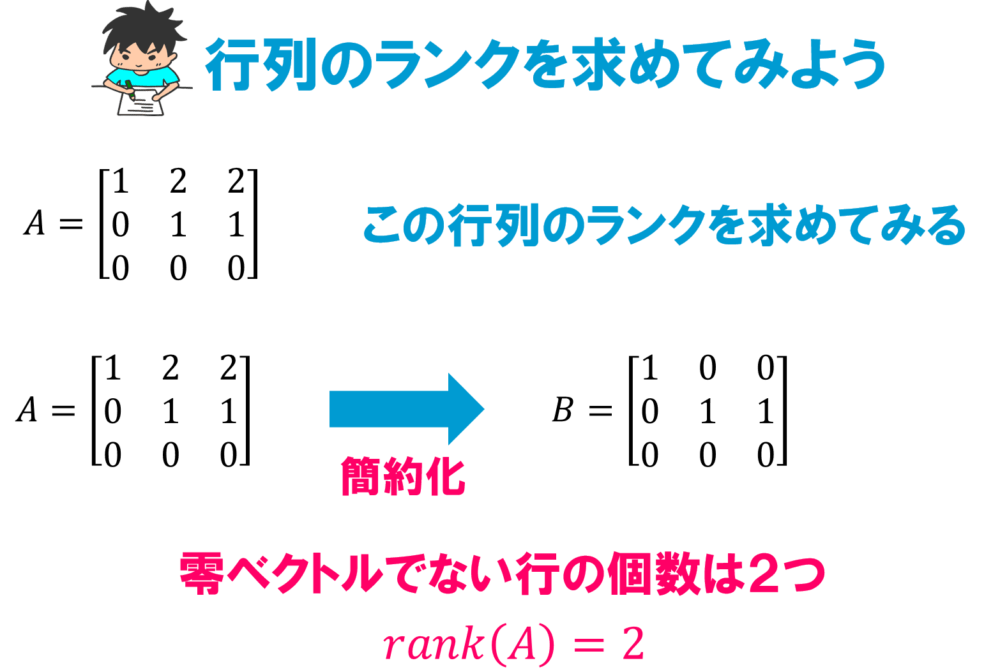

このように簡約化した行列に零ベクトルが含まれる行列をランク落ちした行列と言います。
もし零ベクトルが含まれていなければランクが3だったのに、零ベクトルが1つ含まれているためにランクが3から2に落ちてしまったということでランク落ちした行列と言うんですね。
行列のランクと1次独立の関係性
さて、行列のランクには前回勉強した1次独立と深い関係があります。
それがこちら。
例えば先ほどランクを求めたこちらの行列、実は1次独立な列ベクトルや行ベクトルの数がランクと一致しているんです。
$$\boldsymbol{B} = \left[
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 1 \\
0 & 0 & 0
\end{array}
\right]$$

実際に1次独立なベクトルで1次従属なベクトルを表してみるとこんな感じ。


例えば「行列の中で1次独立な数ベクトルの個数を求めたい」というときは行列を簡約化してランクを調べるだけで求めることができる、といったような使い方ができるわけですね!
正方行列におけるランク
さて、先程はランクと1次独立の関係について見てきましたが、実はランクは逆行列とも深い関係があるんです。
以前の記事で逆行列は存在する場合と存在しない場合があるというお話をしました。
そして、逆行列が存在するかどうかは単位行列を並べた行列を簡約化したときに、単位行列が左側に現れるかどうかで決まるという話もしました。

実はランクを使えば正方行列に逆行列が存在するかどうか調べることができるんです!


ランクを使って調べる方法は至って簡単。
- ランク落ちしてなければ逆行列が存在する
- ランク落ちしていれば逆行列が存在しない
では実際に計算してみましょう!
まずはこちらの行列、逆行列はこのように表されます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
1 & 3 \\
2 & 1 \\
\end{array}
\right] , \boldsymbol{A^{\mathrm{-1}}} = \left[
\begin{array}{rr}
-0.2 & 0.6 \\
0.4 & -0.2 \\
\end{array}
\right]$$
では本当にこの行列\(A\)がランク落ちしていないか調べてみましょう。

では今度は逆行列が存在しない場合を見てみます。
例えばこちらの行列は逆行列が存在しません。
$$\boldsymbol{C} = \left[
\begin{array}{rr}
1 & -2 \\
2 & -4 \\
\end{array}
\right]$$
簡約化してみた結果、左側に単位行列が現れないことからもそれがわかりますね。
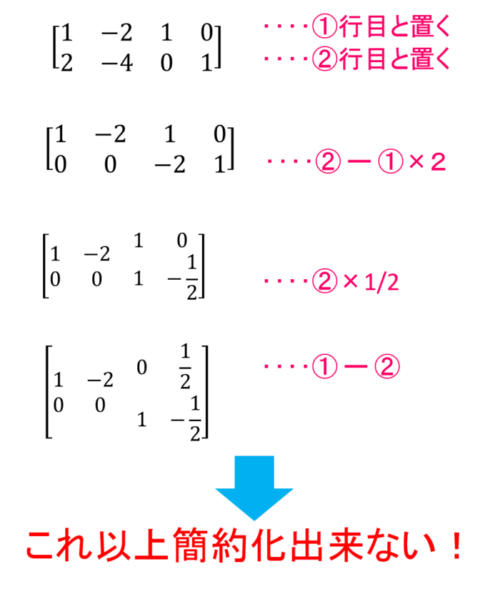
では実際にランクを計算してみるとどうなるでしょうか?

確かにランク落ちしていることがわかりますね!
このように、逆行列が存在するかどうかはランクを調べることによって容易に知ることができるんです。
かなり便利な方法なので覚えておいてくださいね!
まとめ: ランクを調べれば逆行列もわかる
さて、今回は行列のランクについて1次独立、逆行列との関係性を見ながら学んできました。
- 行列のランクとは行列\(A\)を簡約化した行列を\(B\)としたとき\(B\)の零ベクトルでない行の個数
- 行列のランクと1次独立な数ベクトルの最大個数は等しい
- 逆行列の有無はランクを調べればわかる
行列のランクは線形代数でもかなり重要な概念です。
しっかり理解して次のステップに進んでいきましょう!













