

クロネッカーのデルタという名前は聞いたことがある方も多いのではないでしょうか?
線形代数の最初の方で勉強したことがある方もいると思います。
今回はクロネッカーのデルタについて基礎的な内容から内積との関係まで解説。
この記事を読んで更に理解を深めていきましょう!
クロネッカーのデルタってなに?
まずはクロネッカーのデルタがどういうものなのかという所から確認していきましょう。
1 (i=j) \\
0 (i≠j)
\end{cases}\]
例えば\(i=j=1\)や\(i=j=2\)のときには\(1\)になって\(i=1,j=3\)などの場合には\(0\)になるということですね。
\(δ\)はデルタと読みますが、レオポルド・クロネッカーというドイツの数学者が名付けたことでクロネッカーのデルタと言うようになりました。
クロネッカーのデルタと単位行列
ここまでのお話は知っている方もいるかと思います。
では次に少し進んで単位行列との関係を見てみましょう。
まずはこのクロネッカーのデルタに\(i,j=1~3\)のすべての組合せを順に考えていきます。
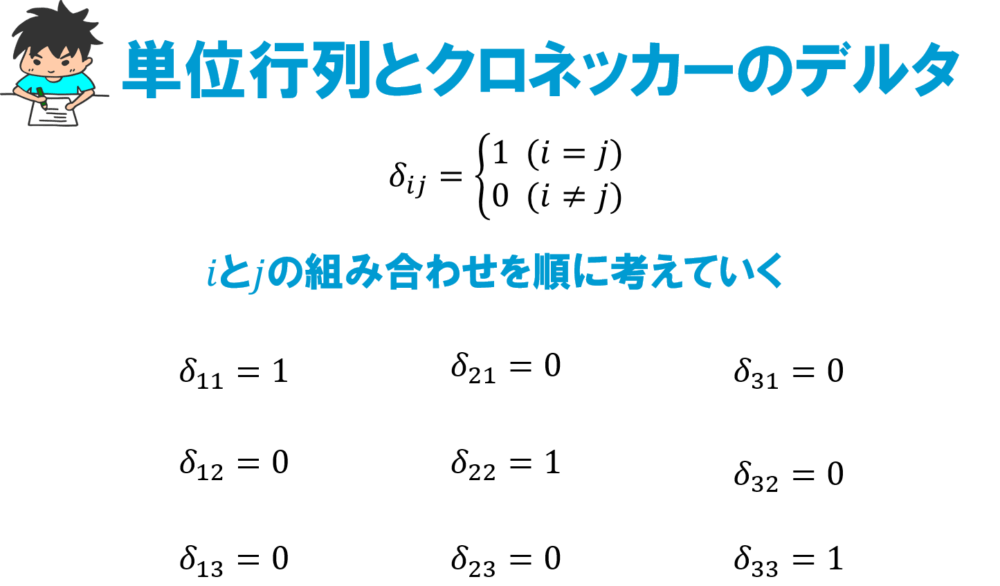

行列の\(i,j\)成分を\(A_{ij}\)と表記すると,単位行列は以下のように表すことができます.


\(i=j\)であるところだけ行列の成分が1になるのが単位行列の特徴なので、このようにクロネッカーのデルタを使って単位行列を表すことが出来るというわけ!
では次にクロネッカーのデルタと内積の関係を見ていきましょう。
クロネッカーのデルタと内積
実は内積もクロネッカーのデルタを使って表現することが出来るんです。
まず簡単のために基本ベクトルの内積をクロネッカーのデルタを使って表してみましょう。
内積についていまいち、、という方はこちらの記事を参考にしてみてください。
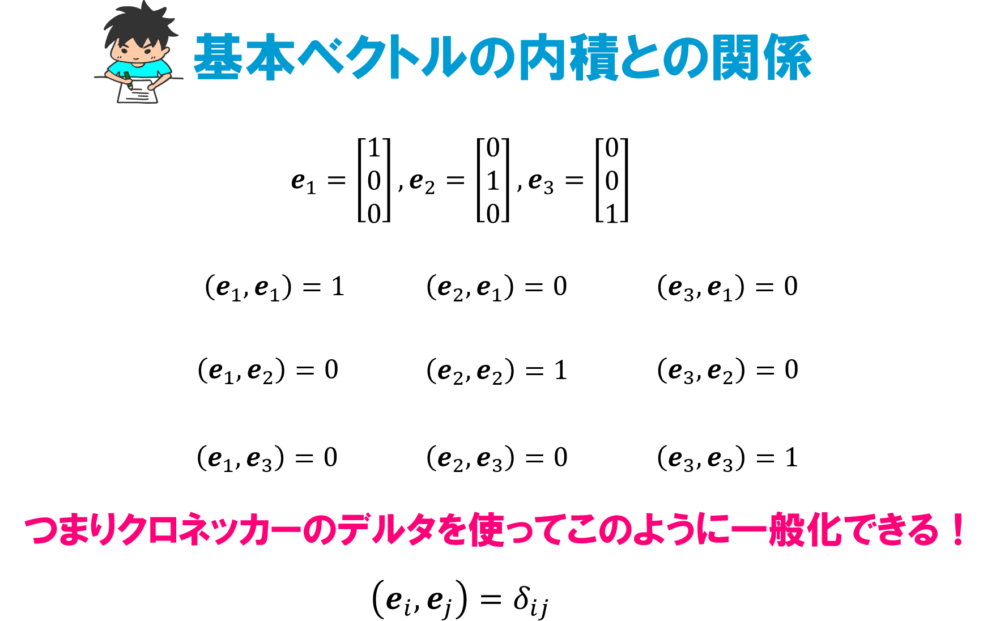
これで基本ベクトルの内積をクロネッカーのデルタで表すことが出来ました。
ではこれをもう少し一般化して普通のベクトルについても考えてみましょう。
まずこのような2つのベクトルを用意します。
$$\boldsymbol{\textbf{a}} = \left[
\begin{array}{r}
a_1\\
a_2\\
a_3 \\
\end{array}
\right],\boldsymbol{\textbf{b}} = \left[
\begin{array}{r}
b_1\\
b_2\\
b_3 \\
\end{array}
\right]$$
これらのベクトルを使って内積を計算してみます。


最後にシグマ記号を外してみます。


以上のことから標準内積もクロネッカーのデルタで表現出来ることが分かりますね!
この導出過程を覚える必要はありませんが、内積とクロネッカーのデルタにはこんな関係があるんだな、くらいに理解していただければオーケーです!
まとめ: 線形代数でたまに出てくる
今回紹介してきた例からもわかるようにクロネッカーのデルタは今まで学んできた単位行列や内積と深い関係があります。
もう一度内容を振り返っておきましょう。
- クロネッカーのデルタ\[δ_{ij}=\begin{cases}
1 (i=j) \\
0 (i≠j)
\end{cases}\] - 単位行列は\(A_{ij}=δ_{ij}\)
- 標準内積は\((\textbf{a} , \textbf{b} )=\sum_{i=1}^{n}\sum_{j=1}^{n}a_ib_jδ_{ij}\)
クロネッカーのデルタは線形代数を勉強していると度々出てきます。
しっかり理解しておきましょう!













