

今回はシュミットの正規直交化という内容について解説していきます。
名前だけ聞くとなんだか複雑そうなのですが、一つ一つ噛み砕いていくとそこまで難しい内容ではないことがわかるはず。
図解も使って分かりやすく解説していくので安心して学んでいきましょう!
直交している大きさが1のベクトルに直すこと
そもそもシュミットの正規直交化って何なのでしょうか?
それを理解するには正規直交化という言葉を「正規化」と「直交化」という2つの言葉に分けて考えてみるとわかりやすいです。
- 正規化とは、あるベクトルの長さを1にすること。ベクトル\(a_1\)を長さ1にするには\(u_1=\frac{a_1}{|a_1|}\)とすればいい
- 直交化とは、あるベクトルとベクトルを直行の関係にすること。直行とは内積が0、すなわち\((a\cdot b=0)\)を満たす事を言う
つまり正規直交化とはいくつかのベクトルたちをすべて長さが1で直行の関係にすることを言います。
これをエルハルト・シュミットさんという方が名付けたのでシュミットの正規直交化と言うんです。

ではどうして正規直交化をわざわざする必要があるのでしょうか?
次のベクトルたちを見てください。
$$\boldsymbol{a} = \left[
\begin{array}{r}
5\\
5 \\
\end{array}
\right],\boldsymbol{b} = \left[
\begin{array}{r}
3\\
1 \\
\end{array}
\right],\boldsymbol{c} = \left[
\begin{array}{r}
1\\
2 \\
\end{array}
\right]$$
ベクトル\(b,c\)は以下の式を満たす定数の組合せが\(c_1=c_2=0\)しか無いので1次独立の関係にあります。
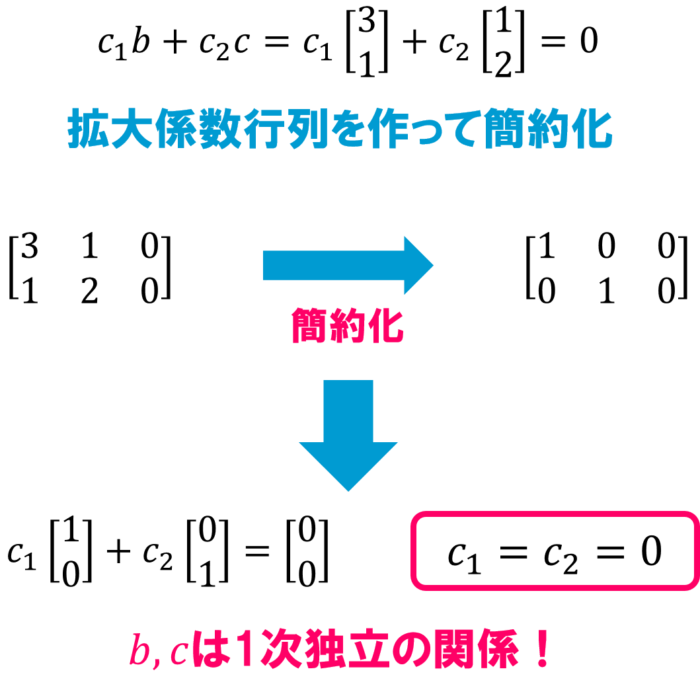
そしてベクトル\(a\)はベクトル\(b\)と\(c\)を使ってこのように表すことが出来ますね。
\[a=b+2c\]
このように1次独立なベクトルを使えば他のベクトルを表すことはできるんですが、ベクトル\(b,c\)はそれぞれ長さがバラバラ。
「どうせなら長さが1で直行するベクトルたちで表したほうが分かりやすいのでは?」という考えが出てきたんです。
ここで先程のシュミットの正規直交化が使えます。
シュミットの正規直交化を使えば長さが1で直行するベクトルたちを作り出すことができるのでとても分かりやすい形で他のベクトルを表すことが可能。
こういった背景があってシュミットの正規直交化は必要とされているわけですね。


図を使いながら手順を理解
シュミットの正規直交化は\(n\)本のベクトルに対して使うことが出来ますが、今回は分かりやすいように3本のベクトルの正規直交化の方法を解説していきます。
例えばベクトル\(a_1,a_2,a_3\)があったとしてこれらのベクトルから長さが1で直行するベクトル\(u_1,u_2,u_3\)を作る方法は以下の通り。
\[u_1=\frac{a_1}{|a_1|}\]
\[v_2=a_2-(a_2\cdot u_1)u_1, u_2=\frac{v_2}{|v_2|}\]
\[v_3=a_3-(a_3\cdot u_1)u_1-(a_3\cdot u_2)u_2, u_3=\frac{v_3}{|v_3|}\]


一見複雑そうな式ですが、実はちゃんとした意味があるんです。
まず式をこのように分類してみます。

実はこの分類は正規化と直交化で分類しているんです。
左側の式たちはもとのベクトルをベクトルの大きさで割っているので長さが1になって正規化しているということが分かりますね。
逆に右側の内積を使った式たちは直交化を表しているということになります。



例えば次の図のようなベクトルの関係を考えてみます。
ベクトル\(a_2\)を使ってベクトル\(a_1\)に平行なベクトル\(t_2\)を求めてみましょう。

これで平行なベクトル\(t_2\)を求めることが出来ました!
では先程の直交化の式と見比べてみましょう。

このように共通部分が出てきました。
これらより直交化の式では平行なベクトルを引いている(直行なベクトルのみを作っている)ということになります。

あとはベクトル\(v_2,v_3\)を先程の正規化の式で長さを1にすれば正規直交化された\(u_2,u_3\)が完成。


では先程の式を使って実際にベクトルを正規直交化してみましょう!
実例を用いて理解しよう
今回は以下のベクトルを正規直交化していきます。
$$\boldsymbol{a_1} = \left[
\begin{array}{r}
1\\
0\\
0 \\
\end{array}
\right],\boldsymbol{a_2} = \left[
\begin{array}{r}
1\\
1\\
0 \\
\end{array}
\right],\boldsymbol{a_3} = \left[
\begin{array}{r}
0\\
1\\
2 \\
\end{array}
\right]$$
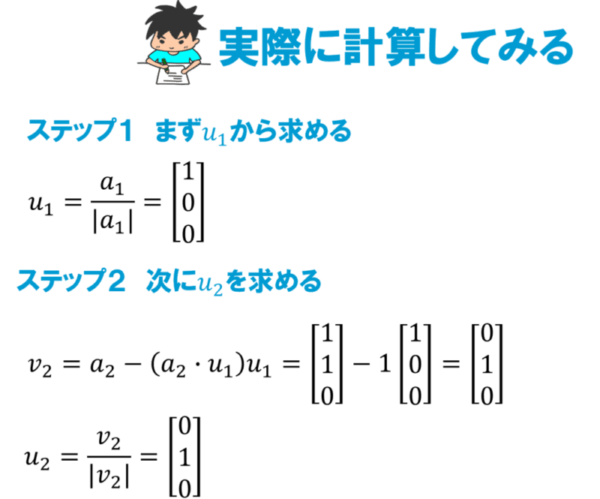


計算結果を見てみると基本ベクトルが出てきていることが分かります。
基本ベクトルは長さが1でお互いに直行するので確かに正規直交化されていることが分かりますね。(実際に内積を計算してみると同じ基本ベクトル同士は1、違う基本ベクトル同士は0になる)

まとめ: 直交化を使うと計算が楽になる
- シュミットの正規直交化とはいくつかのベクトルたちをすべて長さが1で直行の関係にすること。
- 正規化と直交化で式の意味を分けて理解して覚える。
シュミットの正規直交化は計算を楽にするためによく使われます。
ただ、今回は正規直交化がどのようなものなのか、なぜこのような式になるのかを理解できれば完璧。
公式はついつい暗記に走りがちですが、式の意味を理解できれば暗記は一気に楽になります。
しっかり理解しておきましょう!













