行列における「余因子」と「余因子展開」について説明する

今回は余因子と余因子展開について解説していくよ！

少し難しそうな響きだけど頑張る！

さて、今回は余因子と余因子展開について見ていきましょう。

少し複雑そうな感じがしますが、イメージ的には数字遊びに近い内容です。

今まで扱ってきた行列式や逆行列とも関連してくる内容なので頑張って学んでいきましょう！

余因子ってなんなの？

まずは余因子がどういうものなのか、というところから。

ざっくりと言えば、もとの行列の行と列を一つずつ抜き取った小さな行列の行列式にプラスまたはマイナスの符号を付けたもの。

と、言いますと？

次の具体例で計算方法を追っていけばわかると思うよ！

例えば次のような行列があったとして、その余因子を考えてみます。

$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 2 & 3 \\
4 & -5 & 1 \\
1 & 3 & 2
\end{array}
\right]$$

余因子の計算法は？

余因子の計算方法のステップは以下の通り。

さて、最後にプラスかマイナスを付けるのですが、どちらを付けるのか決めるためにはルールがあります。

それがこちら。

今回の例では１行目と２列目を抜き取ったのでその数の合計は３。

よって奇数なのでマイナスを付けます。

これで余因子を求めることができたね！

今回の例では1行目と2列目を抜き取って余因子を計算しましたが、1行目と3列目、2行目を2列目などを抜き取っても余因子を求めることができます。

いろいろな組み合わせを試してみて余因子の計算方法を練習してみましょう！

余因子展開と行列式

余因子の求め方はわかったけど、これって何に使うの？

先程求めた余因子ですが、これを使うともとの行列の行列式を求めることができるんです！

例えば次の行列の行列式を求めたいとします。

$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 3 & 3 \\
0 & 0 & 2 \\
2 & -4 & 5
\end{array}
\right]$$

前回紹介したようなたすき掛けの方法を使えば行列式を求めることはできますが、3行3列の行列式は求めるのが少し複雑でしたよね。

では余因子を使って求めるとどうなるか見てみましょう！

余因子を使って求めていくには余因子展開というものを使って行列式を違う形に書き換えながら求めていきます。

例えば、２行目に関する余因子展開を使えば3×3の行列式もこのような形に書き換えることができるんです。

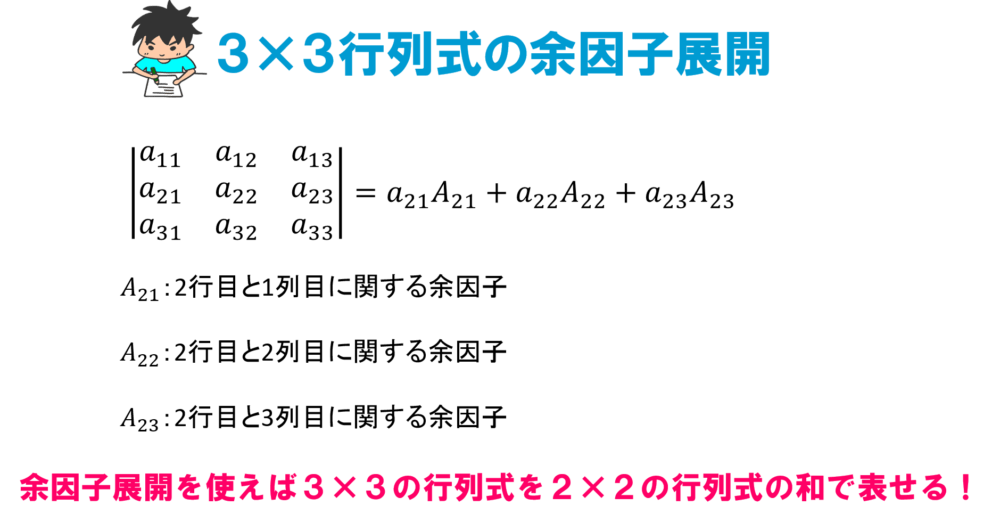
ではこの行列の行列式を余因子展開を使って求めてみましょう。

今回は例として２行目に関する余因子展開をしていきます。

$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 3 & 3 \\
0 & 0 & 2 \\
2 & -4 & 5
\end{array}
\right]$$

余因子展開を使うと計算式がかなり簡単になりましたね！

では、余因子を計算していきます。

これでもとの行列の行列式を求めることができました！

こうしてみると、たすき掛けのときよりも比較的ラクに計算することができましたね。

このように余因子展開を使った行列式の計算方法は行や列に0を多く含む場合に効果的なので覚えておきましょう！

まとめ: 余因子を使えば計算が楽になる！

さて、今回は余因子と余因子展開について見てきました。

今回の内容は行列式を求めるときに有効だし、逆行列を求めるときにも有効なのでしっかりマスターしておきましょう！