

以前、逆行列を掃き出し法を用いて求める方法を解説しました。
しかし、実は逆行列は行列式と余因子を使っても求めることができるんです!
今回はその計算方法を解説していきます。
ではいきましょう!
余因子行列とは?
前回の記事で余因子についてはしっかりと学んできましたね。
余因子とはもとの行列からある行と列を抜き取った行列の行列式にプラスまたはマイナスを付けたものでした。
では、この余因子をすべての行と列に関して計算して新しく行列を作ってみましょう。

見ての通り、すべての成分が余因子から構成されている行列だから余因子行列ということですね。
実は逆行列はこの余因子行列をもとの行列の行列式で割ってあげるとすぐに求めることができるんです!
余因子行列を使った2行2列行列の逆行列の求め方
さて、ではここからは2行2列行列の逆行列を求めていきましょう。
先程の逆行列の求め方を言葉と数式で表すとこんな感じ。

この公式を使って以下の行列の逆行列を求めてみます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
-1 & 2 \\
4 & -5 \\
\end{array}
\right]$$

次に余因子行列を求めます。
2行2列の場合はある行と列を抜き取ると1つの成分だけが残るので余因子行列を求めやすいですね!

では最後に先程の公式に代入して逆行列を求めます。

これで逆行列を求めることができました!
では、次に3行3列の逆行列も計算してもう少し余因子行列を使った逆行列の求め方に慣れていきましょう。
3行3列の逆行列もやり方は同じ
次数が増えても逆行列の求め方は変わりません。
次の行列の逆行列を求めてみましょう。
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 3 & 3 \\
0 & 0 & 2 \\
2 & -4 & 5
\end{array}
\right]$$
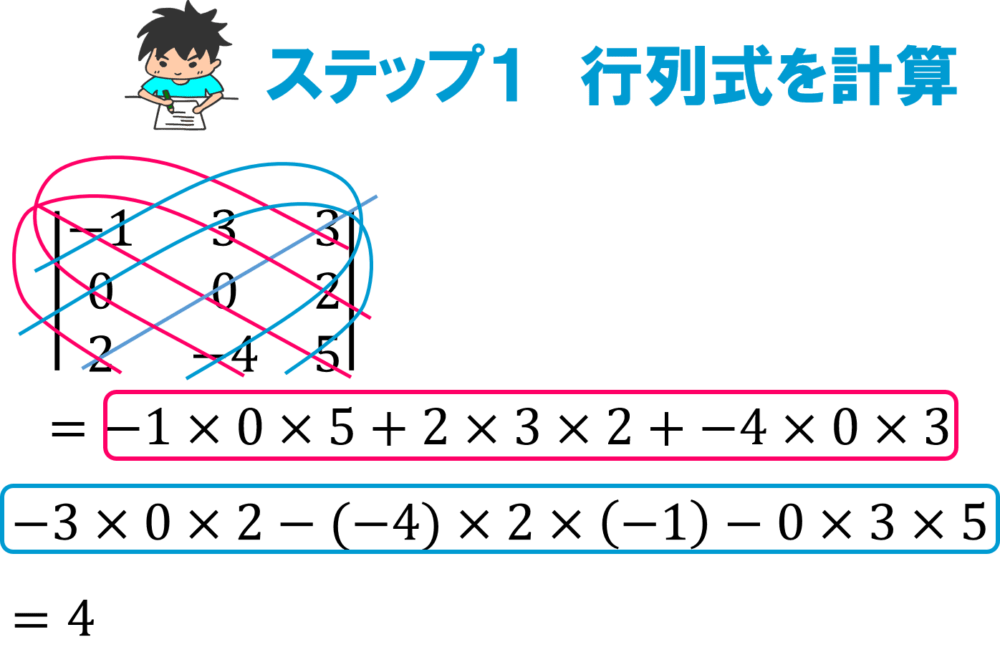
次は余因子行列。
計算が少し面倒ですが、頑張って求めます。

そして最後に公式に当てはめます。


計算が少し多かったですが、2×2行列の時と同じやり方で逆行列を求めることができました。
行列の大きさが増えてくると計算が複雑になってきますが、練習のために一度はこの方法で逆行列を計算してみてくださいね!
まとめ: 行列の大きさでやり方は変えよう
さて、今回は逆行列を行列式と余因子行列を使って求めてきました。
今回紹介した方法は行列が大きくなってくるとあまりおすすめできませんが、うまく使えば掃き出し法よりも早く逆行列を求めることができます。
掃き出し法と適宜使い分けながら逆行列を求めていくのがベストですね。
少しボリュームのある内容だったのでしっかり復習しておきましょう!













