

前回までの内容で逆行列の性質から求め方まで一通り逆行列について学んできました。
今回はその復習として、逆行列を使って実際に連立方程式を解いてみましょう!
逆行列についてしっかり身についているか確認してくださいね。
ではいきましょう!
連立方程式を行列形式に直す
今回解くのはこちらの連立方程式。
\[
\left\{\begin{align}
x_1 + x_2 & = & 2 \\
2x_1 + 3x_2 & = & 5
\end{align}\right.
\]
この連立方程式を逆行列を使って解いていくのですが、まず解く手順を押さえておきましょう。
- 連立方程式を\(Ax=b\)の形に変形
- \(A\)の逆行列を求める
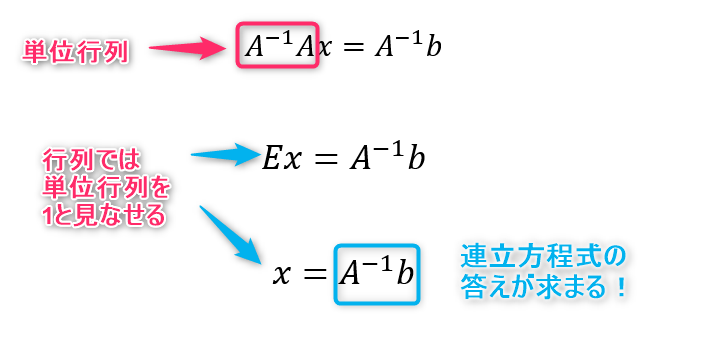
- 両辺に\(A\)の逆行列\(A^{\mathrm{-1}}\)を左側からかける
手順③についてですが、これは\(A\)と\(A^{\mathrm{-1}}\)をかけると単位行列になるという逆行列の性質を使っています。
このように両辺に逆行列\(A^{\mathrm{-1}}\)をかけると左辺が\(x=\)の形になるので連立方程式の答えが求まるということですね!
ではこの手順に従って連立方程式を解いてみましょう!
まずは連立方程式を行列の形に変形します。
\[
\left\{\begin{align}
x_1 + x_2 & = & 2 \\
2x_1 + 3x_2 & = & 5
\end{align}\right.
\]
$$\left[
\begin{array}{rr}
1 & 1 \\
2 & 3 \\
\end{array}
\right]\left[
\begin{array}{rr}
x_1 \\
x_2 \\
\end{array}
\right]
= \left[
\begin{array}{rr}
2 \\
5 \\
\end{array}
\right]$$

逆行列の求め方は覚えていますか?覚えていない方はこちらの記事を参考にしてみてください!
では逆行列を求めていきます。


では最後にこの逆行列を両辺にかけてみましょう!
逆行列を両辺にかける
左辺は元の行列と逆行列のかけ算なので単位行列になりますね。
右辺は計算してみると次のようになります。
$$\boldsymbol{A^{\mathrm{-1}}}\boldsymbol{b} = \left[
\begin{array}{rr}
3 & -1 \\
-2 & 1 \\
\end{array}
\right]\left[
\begin{array}{rr}
2 \\
5 \\
\end{array}
\right]
= \left[
\begin{array}{rr}
1 \\
1 \\
\end{array}
\right]$$
これで答えが求まりました!
\[ \left\{\begin{align} x_1 & = & 1 \\ x_2 & = & 1 \end{align}\right. \]
では実際にこの答えが正しいものなのか、元の連立方程式に代入して確認してみましょう。
\[
\left\{\begin{align}
1 + 1 & = & 2 \\
2×1 + 3×1 & = & 5
\end{align}\right.
\]

これで逆行列を使って連立方程式を求めることが出来ました!
スムーズに理解できたでしょうか?
もしここまでの流れがしっかり理解できたなら連立方程式と逆行列の理解は完璧です!
まとめ:実際に使って慣れていこう
さて、今回は逆行列を使って連立方程式を解いてきました。
今回の内容は今まで学んできた連立方程式や簡約化、逆行列がすべて関係してきます。
ここまでの内容がしっかり理解できている方は安心して次の内容へ、少し曖昧な方はいったん立ち止まって今までの内容を復習してみてください。
「わからない」を無くして一歩ずつ次に進んでいきましょう!













