

前回は行列の簡約化について詳しく見てきました。
今回は実際に行列の簡約化を使って連立方程式を解いていきましょう。
また、矛盾して解けない連立方程式や解が無数に存在する連立方程式についても解説していきます。
ではいきましょう!
通常の連立方程式は簡約化で解ける
ではまずは通常の解が存在する連立方程式を行列の簡約化を使って解いていきましょう。
以下の連立方程式を例に見ていきます。
\[
\left\{\begin{align}
2x + y & = & 9 \\
x + 3y & = & 17
\end{align}\right.
\]
この連立方程式の拡大係数行列はこのように表されるのでした。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
2 & 1 & 9 \\
1 & 3 & 17 \\
\end{array}
\right]$$
この拡大係数行列を行列の基本変形を使って簡約化していきます。


あとはこの拡大係数行列に対応する連立方程式を考えるだけ。
このような連立方程式になりますね。
\[
\left\{\begin{align}
x & = & 2 \\
y & = & 5
\end{align}\right.
\]

これで行列の簡約化を使って連立方程式を解くことが出来ました!
今は2元一次連立方程式を解きましたが、もっと文字数が多くなってくると連立方程式は解くのが難しくなってきます。
そのようなときに行列の簡約化を使った解法は威力を発揮するはずです。
矛盾していて解けない連立方程式がある
先ほどの例では解ける連立方程式を紹介しましたが、実は矛盾していて解けない連立方程式も存在します。
例えば次のような連立方程式です。
\[
\left\{\begin{align}
x + y & = & 1 \\
2x + 2y & = & 4
\end{align}\right.
\]
パッと見ただけでも明らかに矛盾しているのがわかりますね。
ではこの連立方程式の拡大係数行列を簡約化してみましょう。
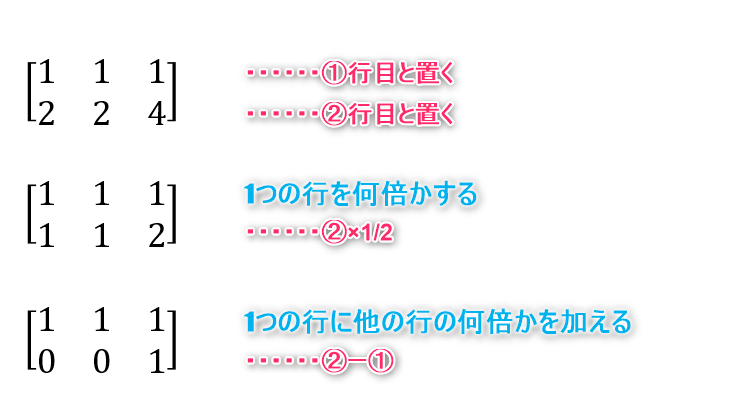
この拡大係数行列を連立方程式に戻してみるとこのようになりますね。
\[ \left\{\begin{align} x + y & = & 1 \\ 0 & = & 1 \end{align}\right. \]
第2式に矛盾した式が出てきてしまいました。
つまりこの連立方程式は解けないということが分かります。
解が無数に出てくる連立方程式がある
さて、もう一つ特殊な連立方程式をご紹介しましょう。
それが解が無数に出てくる連立方程式。
例えばこんな連立方程式です。
\[ \left\{\begin{align} x + y & = & 1 \\ 2x + 2y & = & 2 \end{align}\right. \]


例えば\(x=2\),\(y=-1\)はこの連立方程式を満たすし、\(x=100\),\(y=-99\)でもこの連立方程式を満たしてしまいます。
ではこの連立方程式の拡大係数行列を簡略化してみましょう。

この拡大係数行列を連立方程式に戻してみます。
\[
\left\{\begin{align}
x + y & = & 1 \\
0 & = & 0
\end{align}\right.
\]
第2式は常に成り立っているので実質この連立方程式は\(x+y=1\)のみということになりますね。
この場合未知数が2つなのに対して式が1つしか無いので\(x\)と\(y\)の組み合わせは無数に存在する、つまり解が無数に存在することになります。
まとめ: 連立方程式と行列の関係はバッチリ
さて、今回は連立方程式を拡大係数行列の簡約化を使って解いてきました。
また、解けない連立方程式が存在すること、解が無数に存在する連立方程式があることもご紹介しました。
ここまで来れば連立方程式と行列の関係はバッチリです!
次のステップに向けて引き続き頑張っていきましょう!













