掃き出し法を使って逆行列を求める手順を徹底解説！

今回は実際に逆行列を求めてみよう！

前回まで逆行列の求め方は詳しく触れてなかったから楽しみ！

前回の記事では逆行列の性質について見てきました。

しかし、具体的な逆行列の求め方については解説してきませんでしたね。

今回からはいよいよ逆行列の求め方について見ていきます。

といっても難しいことは全然無くて、今までの知識を使えば逆行列は簡単に求めることができます。

ではいきましょう！

簡約化で逆行列を求める

逆行列を求めるためには行列の基本変形を使って行列を簡約化することによって求めていきます。

行列の基本変形は以下の3つの変形を指すのでした。

では、具体的に逆行列を求めていきましょう！

逆行列を求める手順は以下の通り。

ふむふむ、、？

具体例を見ればすぐ理解できるはずだよ！

今回は以下の行列の逆行列を求めていきます。

$$\boldsymbol{A} = \left[
\begin{array}{rrr}
4 & 2 & 3 \\
2 & 1 & 1 \\
3 & 2 & 3
\end{array}
\right]$$

逆行列を求める手順に従って、まず行列の右側に単位行列を置きます

$$\boldsymbol{B} = \left[
\begin{array}{rrr}
4 & 2 & 3 & 1 & 0 & 0 \\
2 & 1 & 1 & 0 & 1 & 0 \\
3 & 2 & 3 & 0 & 0 & 1
\end{array}
\right]$$

この時、右側に置く単位行列は逆行列を求めたい行列と同じサイズにしてくださいね

この例では逆行列を求めたい行列が\(3\)×\(3\)行列なので、単位行列も\(3\)×\(3\)行列になります。

この行列を簡約化して左側の行列を単位行列に変形していきます。

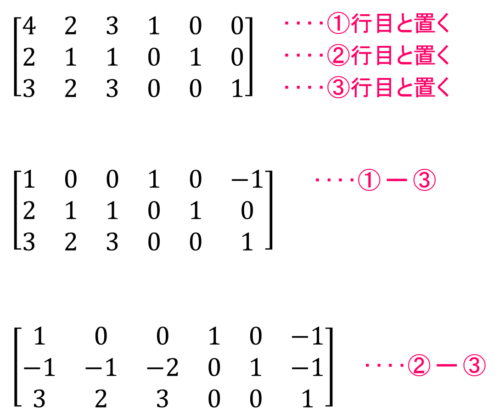
簡約化を使って左側の行列を単位行列に変形することができたね！

これで右側に現れた行列が逆行列になります。

つまり逆行列は、

$$\boldsymbol{A^{\mathrm{-1}}} = \left[
\begin{array}{rrr}
1 & 0 & -1 \\
-3 & 3 & 2 \\
1 & -2 & 0
\end{array}
\right]$$

簡約化するだけで逆行列を求めることが出来るんだね！

これが逆行列を求める手順。

こうやって具体例を見てみると逆行列を求めるには今まで学んできた簡約化を使えばいいだけということが分かりますね！

元の行列と逆行列をかける

さて、ここで先ほど求めた逆行列が本当に元の行列の逆行列なのか確認してみましょう。

逆行列の性質は元の行列と逆行列をかけると単位行列になるというものでした。

実際にかけ算してみましょう。

$$\boldsymbol{A}\boldsymbol{A^{\mathrm{-1}}} = \left[
\begin{array}{rrr}
4 & 2 & 3 \\
2 & 1 & 1 \\
3 & 2 & 3
\end{array}
\right]\left[
\begin{array}{rrr}
1 & 0 & -1 \\
-3 & 3 & 2 \\
1 & -2 & 0
\end{array}
\right] = \left[
\begin{array}{rrr}
1 & 0 & 0 \\
0 & 1 & 0\\
0 & 0 & 1\\
\end{array}
\right]$$

ちゃんと単位行列が出てきた！

これで先ほど求めた逆行列が本当に元の行列の逆行列か確認することが出来ました。

逆行列が存在しない場合は？

先ほどの例では逆行列が存在する場合を見てきました。

では逆行列が存在しない場合はどうでしょうか？

例として以下の行列を考えてみます。

$$\boldsymbol{A} = \left[
\begin{array}{rr}
1 & -2 \\
2 & -4 \\
\end{array}
\right]$$

右側に\(2\)×\(2\)の単位行列を並べて簡約化してみます。

簡約化してみた結果、左側に単位行列を作れないことがわかったね。

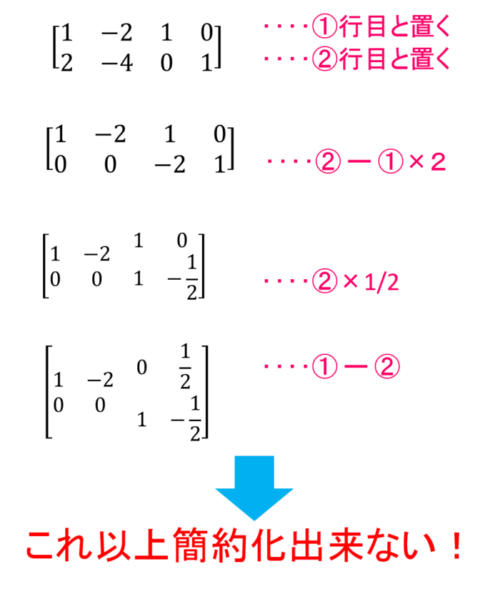
このように簡約化して左側に単位行列が現れない時、元の行列には逆行列が存在しないことになります。

まとめ：逆行列は数字遊びのように求められる

さて、今回は逆行列の求め方を具体例を使いながら見てきました。

もう一度今回の内容を振り返ってみましょう。

逆行列を求めるといっても基本変形を使って行列を簡約化しているだけ。

言うなれば数字遊びのようなものです。

今回の内容も重要なのでしっかりマスターしておきましょう！