

行列の簡約化と聞くとなんだか難しそうな感じがしますが、実はそんなに難しくないんです。
また、簡約化は線形代数でもよく使うのでしっかりマスターしておくことが大事です。
ではさっそく、具体例を使いながら簡約化について見ていきましょう!
連立1次方程式をスッキリさせる
行列の簡約化について解説する前にまずは連立方程式をスッキリ綺麗にすることから解説して、その後に行列の簡約化を見ていきます。


では以下の連立方程式の変数を減らしてスッキリ綺麗にしてみましょう!
\[
\left\{\begin{align}
2x + 2y + 2z & = & 4 \\
y + 2z & = & 1 \\
\end{align}\right.
\]

変数を減らすことで連立方程式をスッキリ綺麗にできました。
これを行列にも適応していって行列を簡約化していきます。
簡約な行列とは何か
まず簡約化された行列を簡約な行列と言いますが、それがいったいどのようなものなのかというところから押さえておきましょう。
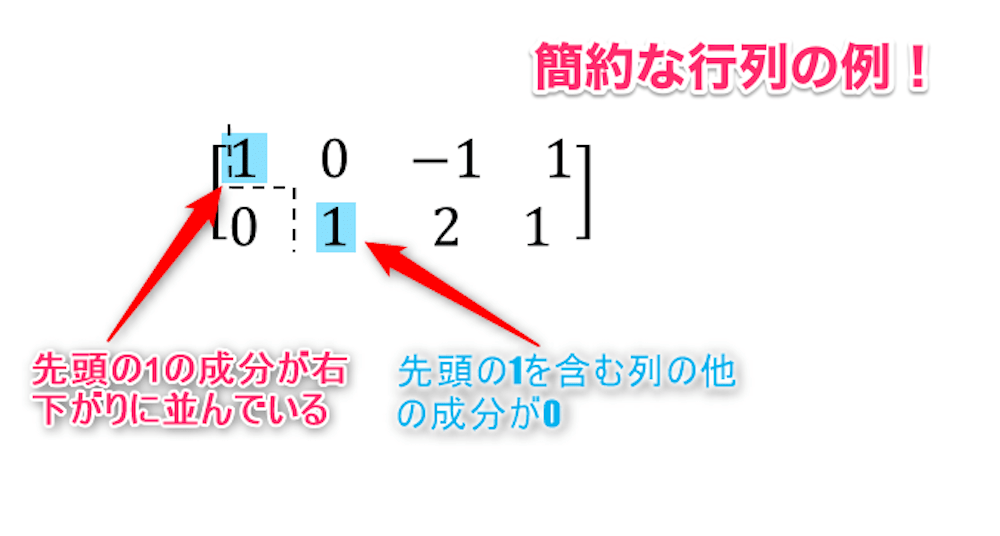
- 行の0以外の先頭の成分が1で、その成分を含む列の他の成分が0であるような行列
- 先頭の1の成分は右下がりに並んでいる
具体的には,以下のような行列が『簡約な行列』です。
先ほどの連立方程式とその拡大係数行列を使って具体例を見ていきます。
まずは先ほどの連立方程式の拡大係数行列を用意して同じように行列を綺麗スッキリしていきます。
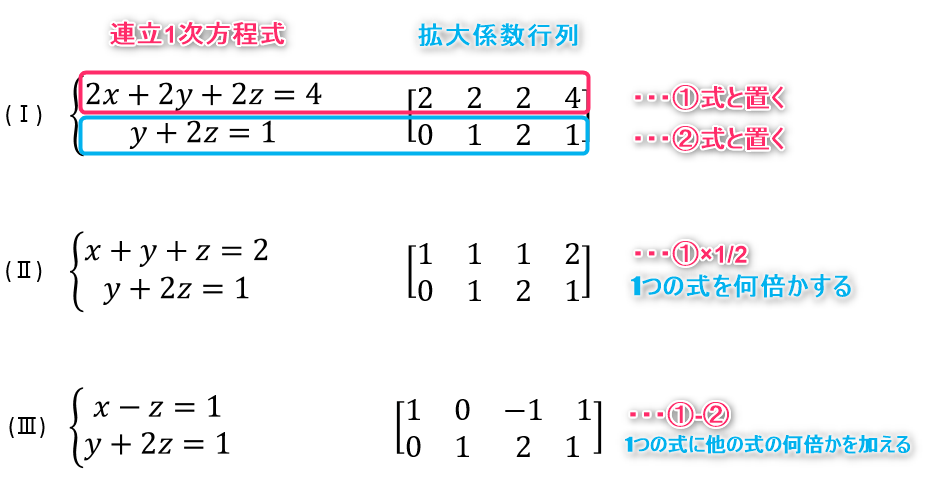

今この行列は簡約化されている状態です。
先ほど説明したように
- 行の0以外の先頭の成分が1で、その成分を含む列の他の成分が0であるような行列
- 先頭の1の成分は右下がりに並んでいる
という簡約な行列の条件を満たしていますね!
そして、拡大係数行列を簡約化することは先ほど説明した『連立方程式を簡単な形にすること』と対応していることも分かりますね。
この簡約化という方法を使えば連立方程式を簡単に解くことが出来るし、後々線形代数を勉強していくうえでもとても重要になってきます!
簡約化の方法を解説
簡約化の方法はいたって簡単、行列の基本変形を使うだけです。
- 1つの行を何倍かする(0倍は含まない)
- 2つの行を入れ替える
- 1つの行に他の行の何倍かを加える
この3つの変形を使えば行列の簡約化を行うことが出来ます!
まとめ: 簡約化は結構使うよ!
さて、今回は行列の簡約化について見てきました。
- 簡約化とは基本変形を使って行列や連立方程式を簡単な形にすること
- 簡約化を使えば連立方程式は簡単に解くことが出来る
この2つのポイントが押さえられていればオーケーです!













