

行列と連立方程式が関連していること、連立方程式を解くことと行列の方程式を解くことは同じであることは前回説明しました。
今回からは実際に行列を使って連立方程式を解く手順を見ていきます。
あまり難しい操作は無いので最後まで安心してついてきてください。
ではいきましょう!
連立1次方程式の解き方と行列の関係を解説する
まずは連立1次方程式を解く手順を解説した後、それを行列にも適応するといった形で説明していきます。


では以下の連立1次方程式を解いていきましょう!
\[
\left\{\begin{align}
3x_1 + 2x_2 & = & 9 \\
2x_1 + x_2 & = & 5
\end{align}\right.
\]
解く手順は普段あまり意識しないかもしれないですが、今回は連立1次方程式の基本変形を使って解いていきましょう。
- 1つの式を何倍かする(0倍は含まない)
- 2つの式を入れ替える
- 1つの式に他の式の何倍かを加える
この3つの基本変形を使って先ほどの連立1次方程式を解いていきます。

①と②はその一つ前の連立1次方程式の第1式、第2式を表しています。

行列を解くときも同じような基本変形を使って解いていきます。
行列に当てはめるとどうみえるか?
先ほどの基本変形を行列に当てはめていきます。
そのための下準備として以下の行列を用意します。
$$\boldsymbol{A} = \left[ \begin{array}{rrr} 3 & 2 & 9 \\ 2 & 1 & 5 \\
\end{array} \right]$$
ちょうど連立方程式の係数を並べたものになりますね。
これを拡大係数行列と言います。
この拡大係数行列に先ほどの変形を当てはめていきましょう。

見て分かるように、連立1次方程式と行列の変形が対応していますね。
そして左側が単位行列、右側が連立1次方程式の解になっていることが分かります。
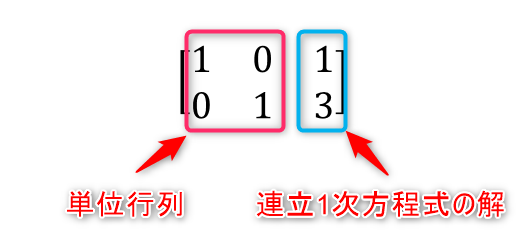
このように行列で連立1次方程式を解くにはまず拡大係数行列に基本変形を使って単純な形に変形し、その単純な行列を拡大係数行列とする連立1次方程式を解けばいいということですね。
行列の基本変形
先ほど連立1次方程式の基本変形を紹介しましたが、行列の基本変形についても同じ。
- 1つの行を何倍かする(0倍は含まない)
- 2つの行列を入れ替える
- 1つの行に他の行の何倍かを加える
この3つの変形を使えば行列を使って連立1次方程式が解けるということですね!
まとめ: うまく使えば連立方程式を効率的に解ける
さて、今回は連立方程式を行列を使って解く方法について見てきました。
行列を使えば連立方程式の係数のみに着目して解くことが出来るのでより効率的に解くことが出来るわけです。
連立方程式を行列で解くというプロセスは線形代数でも重要な内容なのでしっかりマスターしておきましょう!













