

今回から行列式というものを取り扱っていきます。
行列式は線形代数の中でもかなり重要な内容。
しかし、基本を押さえればあまり難しいものでは無いので安心して付いてきてください。
ではいきましょう!
「行列式」の計算方法をみてみよう
行列式の意味は後ほど図を使いながら解説していくとして、まずは行列式の計算方法から見ていきましょう!
行列式という名前ですが、正方行列に対して定義される量というふうに理解してもらった方が分かりやすいはず。
まずは計算例を見ていきましょう。
今回は以下の2次正方行列を考えます。
$$\boldsymbol{A} = \left[
\begin{array}{rr}
-1 & 2 \\
4 & -5 \\
\end{array}
\right]$$
この行列の行列式を計算していきます。
計算方法としてはたすき掛けをイメージしてもらえると分かりやすいですね。
このように左上から右下へかけたものと右上から左下へかけたものの『差を取る』ことによって求めることが出来ます。
以下の具体例で出てくる引き算は,『差を取る』という計算によって出てきているものになります.
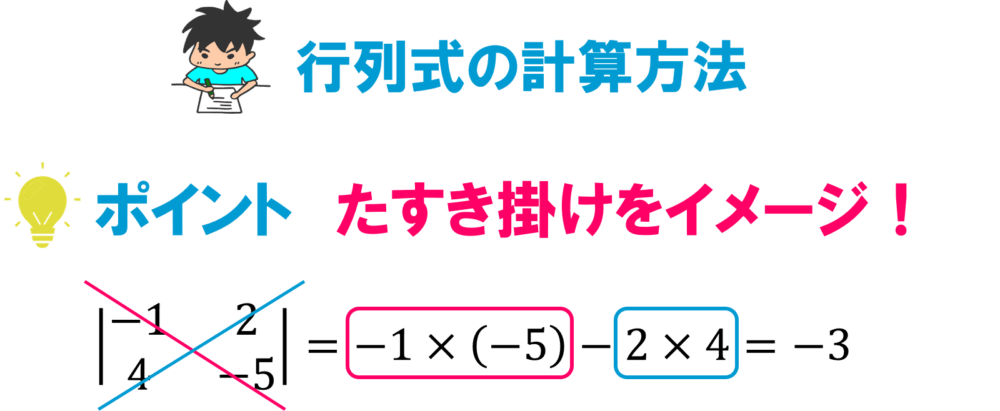


この例からも分かると思いますが、行列式は正方行列に対して定義される量を計算するというふうに考えると分かりやすいですね!
3×3の行列式の計算方法は?
では次に3×3の行列式を計算してみましょう。
この行列を例に計算してみます。
$$\boldsymbol{A} = \left[
\begin{array}{rrr}
-1 & 2 & 3 \\
4 & -2 & 1 \\
1 & 4 & 5
\end{array}
\right]$$
3×3の正方行列でも同様にたすき掛けのイメージで計算していきますが、こちらは少し複雑。
ただ、左上から右下へかけたものと右上から左下へかけたものの差というのは変わりません。
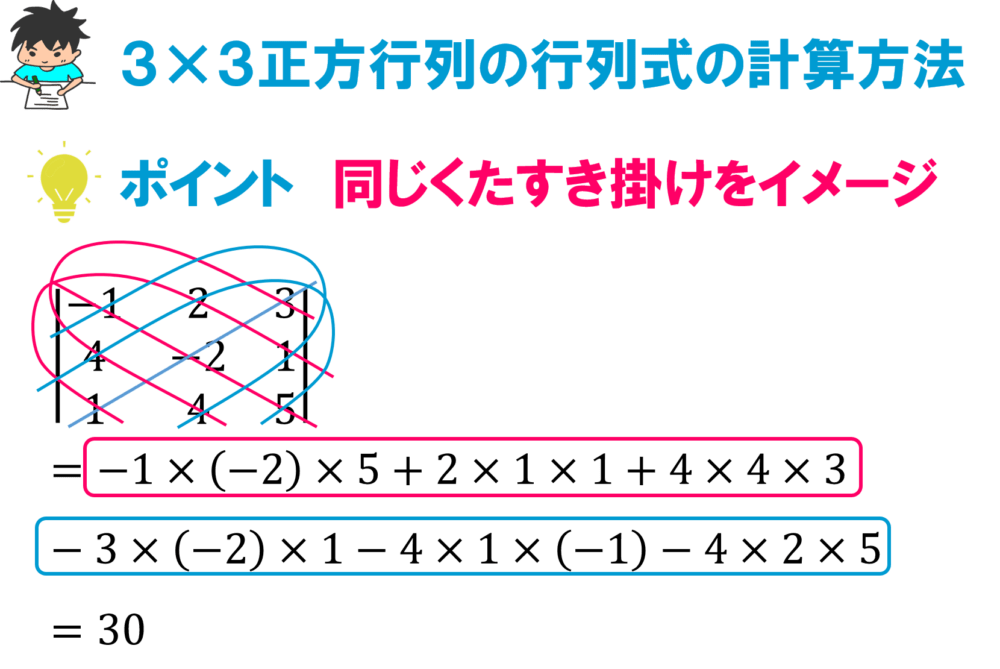

\)や\(|A| = ○○\)のように表します。行列はかぎカッコ\([〇]\)を使いますが、行列式では縦棒\(|〇|\)を使うことに注意してください。
例えば行列が
$$\boldsymbol{A} = \left[
\begin{array}{rr}
-1 & 2 \\
4 & -5 \\
\end{array}
\right]$$
なら行列式は
\[
|A| =
\left|
\begin{array}{cc}
-1 & 2\\
4 & -5
\end{array}
\right| = -3
\] という具合です。
行列式の図形的な意味
さて、ここまで行列式の計算方法を見てきました。
でも行列式っていったい何なのでしょうか?
とりあえず「正方行列に関する量」ということは分かりましたが、どうせならその意味を理解しておきたいですよね。
実は2×2行列の行列式は平行四辺形の面積と関係しているんです!


まずはこのように2つのベクトルからなる平行四辺形を考え、その面積を求めてみます。
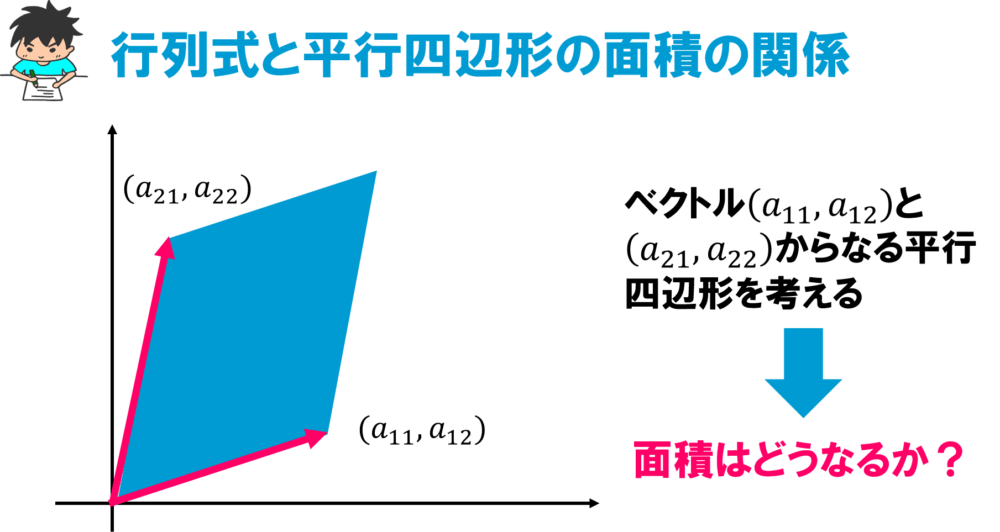
この面積を長方形や直角三角形を使って表していきます。
図形で考えると面積はこのような式で求められますね。

これをベクトルを使った計算に落とし込んでみましょう。
各長方形や直角三角形の面積はそれぞれ次の式で与えられます。
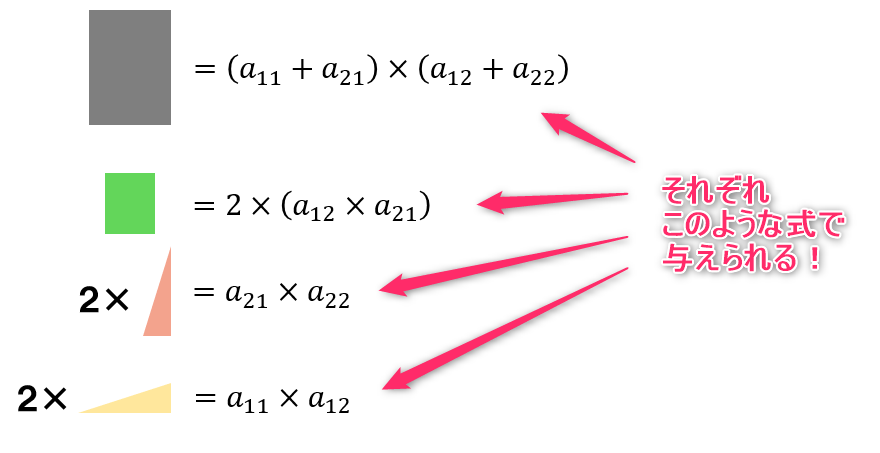
これでそれぞれの図形の面積を求めることが出来ました!
では、平行四辺形の面積を求めていきましょう!



これが2×2行列の行列式の図形的意味。
このように図で対応させてみると、ただの正方行列の量だった行列式も見え方が変わってきますね!
ちなみに3×3行列の行列式は平行六面体の体積に対応します。興味のある方は調べてみると面白いですよ。
このように式の意味もセットで覚えておくとより深い理解に繋がるはずです。
まとめ: 反復練習での慣れが大事!
さて、今回は行列式の計算方法とその図形的意味について図をたくさん使いながら見てきました。
今回の内容をもう一度振り返ってみましょう。
- 行列式は正方行列に定義される量と理解する
- 行列式の計算はたすき掛けをイメージ!
- 2×2行列の行列式は平行四辺形の面積に対応
今回の内容は今後もかなり重要になってくるのでしっかりマスターしておきましょう!













